Day 1: Trebuchet?!
Rust solution to AoC|2023|1.
Input
No separate input processing today. Just operate on the raw character data.
Star 1
The solution consists of two parts:
-
A
map_1function, that returns for any&strthe value of the digit at its head wrapped in anOptionorNoneif there is no digit. -
A
scorefunction which calculates the score for a line by finding the first and last digit. Themap_1function is passed as an argument. -
A
starfunction which calculates the solution by summing over the scores for each line. This function takes as wellmap_1as an argument.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
pub fn map_1(line: &str) -> Option<SolT> {
let b = line.as_bytes()[0];
match b {
b'0'..=b'9' => Some((b - b'0') as _),
_ => None,
}
}
fn score<F: Fn(&str) -> Option<SolT>>(l: &str, f: &F) -> SolT {
(0..l.len()).map(|k| &l[k..]).find_map(f).unwrap() * 10
+ (0..l.len()).rev().map(|k| &l[k..]).find_map(f).unwrap()
}
pub fn star<F: Fn(&str) -> Option<SolT>>(data: &str, map: &F) -> SolT {
data.lines().map(|line| score(line, map)).sum()
}
Catches for the 1st star:
-
There may be lines with only one digit. In that case, it is the first and the last digit.
Star 2
All that is needed for the second star is to extend map_1 function to map_2
1
2
3
4
5
6
7
const DIGITS: [&str; 10] = [
"zero", "one", "two", "three", "four", "five", "six", "seven", "eight", "nine",
];
pub fn map_2(line: &str) -> Option<SolT> {
map_1(line).or_else(|| DIGITS.iter().position(|digit| line.starts_with(digit)))
}
Catches for the 2nd star:
-
Textual representation of digits may overlap like in oneight (this is not an issue when searching from the end of the string, my initial solution just searched for all digits in a line and skipped characters belonging to one digit for the next step)
Tests
Just check the scores for the sample data.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#[cfg(test)]
mod tests {
use super::*;
const CONTENT_1: &str = r#"1abc2
pqr3stu8vwx
a1b2c3d4e5f
treb7uchet
"#;
#[test]
pub fn test_star_1() {
assert_eq!(142, star(CONTENT_1, &map_1));
}
const CONTENT_2: &str = r#"two1nine
eightwothree
abcone2threexyz
xtwone3four
4nineeightseven2
zoneight234
7pqrstsixteen
"#;
#[test]
pub fn test_star_2() {
assert_eq!(281, star(CONTENT_2, &map_2));
}
}
Day 2: Cube Conundrum
Rust solution to AoC|2023|2.
Input
As it is the case quite often, parsing the input was the biggest part of today’s puzzle. Maybe I should stop separate parsing the input and solving the challenge and just do it in one pass?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
pub mod input {
use crate::SolT;
#[derive(Debug)]
pub struct PuzzleData(pub Vec<Vec<[SolT; 3]>>);
fn parse_draw(line: &str) -> [SolT; 3] {
line.split(", ").fold([0; 3], |[r, g, b], color| {
match color
.split_once(' ')
.map(|(n, c)| (n.parse::<SolT>().unwrap(), c))
{
Some((n, "red")) => [r + n, g, b],
Some((n, "green")) => [r, g + n, b],
Some((n, "blue")) => [r, g, b + n],
_ => panic!("Unexpected draw."),
}
})
}
fn parse_game(line: &str) -> Vec<[SolT; 3]> {
line.split_once(": ")
.unwrap()
.1
.split("; ")
.map(parse_draw)
.collect()
}
impl<T: AsRef<str>> From<T> for PuzzleData {
fn from(s: T) -> Self {
PuzzleData(s.as_ref().lines().map(parse_game).collect())
}
}
}
Star 1
iter (enumerated) … filter … map … sum
1
2
3
4
5
6
7
8
9
10
11
pub fn star_1(PuzzleData(games): &PuzzleData) -> SolT {
games
.iter()
.enumerate()
.filter(|(_, game)| {
game.iter()
.all(|[r, g, b]| *r <= 12 && *g <= 13 && *b <= 14)
})
.map(|(pos, _)| pos + 1)
.sum()
}
Star 2
iter … map (nested iter … fold) … map … sum
1
2
3
4
5
6
7
8
9
10
11
12
pub fn star_2(PuzzleData(games): &PuzzleData) -> SolT {
games
.iter()
.map(|game| {
game.iter()
.fold([0; 3], |[r_max, g_max, b_max], [r, g, b]| {
[r_max.max(*r), g_max.max(*g), b_max.max(*b)]
})
})
.map(|[r, g, b]| r * g * b)
.sum()
}
Tests
I proudly announce: all tests passed the first time I executed (normally, I never miss any occasion to do stupid mistakes)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"Game 1: 3 blue, 4 red; 1 red, 2 green, 6 blue; 2 green
Game 2: 1 blue, 2 green; 3 green, 4 blue, 1 red; 1 green, 1 blue
Game 3: 8 green, 6 blue, 20 red; 5 blue, 4 red, 13 green; 5 green, 1 red
Game 4: 1 green, 3 red, 6 blue; 3 green, 6 red; 3 green, 15 blue, 14 red
Game 5: 6 red, 1 blue, 3 green; 2 blue, 1 red, 2 green
"#;
#[test]
pub fn test_from() {
let expected: Vec<Vec<[SolT; 3]>> = vec![
vec![[4, 0, 3], [1, 2, 6], [0, 2, 0]],
vec![[0, 2, 1], [1, 3, 4], [0, 1, 1]],
vec![[20, 8, 6], [4, 13, 5], [1, 5, 0]],
vec![[3, 1, 6], [6, 3, 0], [14, 3, 15]],
vec![[6, 3, 1], [1, 2, 2]],
];
let PuzzleData(games) = PuzzleData::from(CONTENT);
assert_eq!(expected, games);
}
#[test]
pub fn test_star_1() {
assert_eq!(8, star_1(&CONTENT.into()));
}
#[test]
pub fn test_star_2() {
assert_eq!(2286, star_2(&CONTENT.into()));
}
}
Day 3: Gear Ratios
Rust solution to AoC|2023|3.
Input
I just read the input into a grid. To simplify handling at the boundary, a layer of empty space ('.') is added around the original data.
Star 1
I created a helper function numbers that returns an iterator over all numbers in the input data with the help of the next_number function. Actually, the iterator returns a tuple with the number’s value, its position in the grid, and its length (number of digits).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
pub fn numbers(grid: &Grid) -> impl Iterator<Item = (SolT, usize, usize)> + '_ {
successors(next_number(grid, 0), |(_, pos, len)| {
next_number(grid, pos + len)
})
}
pub fn next_number(grid: &Grid, offset: usize) -> Option<(SolT, usize, usize)> {
grid.data()[offset..]
.iter()
.position(|b| b.is_ascii_digit())
.map(|pos| {
grid.data()[offset + pos..]
.iter()
.take_while(|b| b.is_ascii_digit())
.fold((0, offset + pos, 0), |(val, pos, len), &b| {
(10 * val + (b - b'0') as SolT, pos, len + 1)
})
})
}
For every number, we need to check all adjacent positions in the input data, so I created another helper function run_around, which iterates over all adjacent positions (by chaining iterators looking above, to the right, below, and to the left):
1
2
3
4
5
6
7
8
9
10
11
pub fn run_around((col, row): (usize, usize), len: usize) -> impl Iterator<Item = (usize, usize)> {
(col - 1..col + len + 1)
.map(move |col| (col, row - 1))
.chain(once((col + len, row)))
.chain(
(col - 1..col + len + 1)
.rev()
.map(move |col| (col, row + 1)),
)
.chain(once((col - 1, row)))
}
With those helpers in place, the solution for the first star is obtained by filtering out all numbers that are not adjacent to a symbol and summing their values:
1
2
3
4
5
6
7
8
9
10
pub fn star_1(PuzzleData(grid): &PuzzleData) -> SolT {
numbers(grid)
.filter(|(_, pos, len)| {
run_around(grid.to_col_row(*pos), *len)
.map(|pos| grid[pos])
.any(|b: u8| b != b'.' && !b.is_ascii_digit())
})
.map(|(value, _, _)| value)
.sum()
}
Star 2
The second star makes use of the same helper functions as the first star. I first iterate through all the numbers to create a map of the positions of the gear ratio symbols '*' to lists of adjacent numbers. Then I iterate through this map, filter out all entries that do not have exactly two numbers in the list, map to the product of those two numbers, and take the sum.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
pub fn star_2(PuzzleData(grid): &PuzzleData) -> SolT {
numbers(grid)
.fold(HashMap::<_, Vec<_>>::new(), |map, (value, pos, len)| {
run_around(grid.to_col_row(pos), len)
.filter(|&pos| grid[pos] == b'*')
.fold(map, |mut map, pos| {
map.entry(pos).or_default().push(value);
map
})
})
.values()
.filter(|values| values.len() == 2)
.map(|values| values[0] * values[1])
.sum()
}
Tests
As usual.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"467..114..
...*......
..35..633.
......#...
617*......
.....+.58.
..592.....
......755.
...$.*....
.664.598..
"#;
const WIDTH_0: usize = 10;
const HEIGHT_0: usize = 10;
const WIDTH_EXT: usize = WIDTH_0 + 2;
const HEIGHT_EXT: usize = HEIGHT_0 + 2;
#[test]
pub fn test_from() {
let PuzzleData(grid) = PuzzleData::from(CONTENT);
assert_eq!(WIDTH_EXT, grid.width());
assert_eq!(HEIGHT_EXT, grid.height());
}
#[test]
pub fn test_next_number() {
let PuzzleData(grid) = PuzzleData::from(CONTENT);
println!("{:?}", grid);
assert_eq!(Some((467, WIDTH_EXT + 1, 3)), next_number(&grid, 0));
assert_eq!(
Some((35, 3 * WIDTH_EXT + 3, 2)),
next_number(&grid, 2 * WIDTH_EXT)
);
}
#[test]
pub fn test_star_1() {
assert_eq!(4_361, star_1(&CONTENT.into()));
}
#[test]
pub fn test_star_2() {
assert_eq!(467_835, star_2(&CONTENT.into()));
}
}
Day 4: Scratchcards
Rust solution to AoC|2023|4.
Input
Today, I directly operate on the input as &str, no pre-processing.
Star 1
I build an iterator which yields for every line the number of items that appear in both lists on the scratch card using a hash set. Then I apply the scoring function to those numbers and take the sum:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
pub fn count_winners(data: &str) -> impl Iterator<Item = SolT> + '_ {
data.lines()
.map(|line| {
line.split_once(':')
.and_then(|(_, tail)| tail.split_once('|'))
.unwrap()
})
.map(|(lhs, rhs)| {
let lhs = lhs.split_ascii_whitespace().collect::<HashSet<_>>();
rhs.split_ascii_whitespace()
.filter(|value| lhs.contains(value))
.count()
})
}
pub fn star_1(data: &&str) -> SolT {
count_winners(data)
.map(|c| match c {
0 => 0,
n => 1 << (n - 1),
})
.sum()
}
Star 2
I pass through all cards once to update the number of subsequent cards. Since the outer fold does not know the total number of cards, I need to initialize enough counters with 1 (initially, every card is available once).
A key statement from the puzzle description for the algorithm to work is "Cards will never make you copy a card past the end of the table."
1
2
3
4
5
6
7
8
9
10
11
12
13
pub fn star_2(data: &&str) -> SolT {
count_winners(data)
.enumerate()
.fold((0, vec![]), |(sum, mut counts), (pos, wins)| {
counts.resize(counts.len().max(pos + wins + 1), 1);
let cur_count = counts[pos];
for upd_count in &mut counts[pos + 1..=pos + wins] {
*upd_count += cur_count;
}
(sum + cur_count, counts)
})
.0
}
Tests
Nothing special here.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"Card 1: 41 48 83 86 17 | 83 86 6 31 17 9 48 53
Card 2: 13 32 20 16 61 | 61 30 68 82 17 32 24 19
Card 3: 1 21 53 59 44 | 69 82 63 72 16 21 14 1
Card 4: 41 92 73 84 69 | 59 84 76 51 58 5 54 83
Card 5: 87 83 26 28 32 | 88 30 70 12 93 22 82 36
Card 6: 31 18 13 56 72 | 74 77 10 23 35 67 36 11
"#;
#[test]
pub fn test_count_winners() {
assert_eq!(
vec![4, 2, 2, 1, 0, 0],
count_winners(CONTENT).collect::<Vec<_>>()
);
}
#[test]
pub fn test_star_1() {
assert_eq!(13, star_1(&CONTENT));
}
#[test]
pub fn test_star_2() {
assert_eq!(30, star_2(&CONTENT));
}
}
Day 5: If You Give A Seed A Fertilizer
Rust solution to AoC|2023|5.
Input
The parsed input is a struct with a field seeds representing the seeds to be planted and a field 'maps'. The latter is a list of a list of mappings that explains which type of target item type to use with each source item type.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
type Map = (SolT, SolT, SolT);
pub mod input {
use crate::*;
#[derive(Debug)]
pub struct PuzzleData {
pub seeds: Vec<SolT>,
pub maps: Vec<Vec<Map>>,
}
fn parse_ranges(ranges: &str) -> Map {
let mut numbers = ranges.split_ascii_whitespace().map(str::parse);
(
numbers.next().unwrap().unwrap(),
numbers.next().unwrap().unwrap(),
numbers.next().unwrap().unwrap(),
)
}
fn parse_group(group: &str) -> Vec<Map> {
group.lines().skip(1).map(parse_ranges).collect()
}
impl<T: AsRef<str>> From<T> for PuzzleData {
fn from(s: T) -> Self {
let mut groups = s.as_ref().split("\n\n");
Self {
seeds: groups
.next()
.and_then(|group| group.strip_prefix("seeds: "))
.and_then(|seeds| {
seeds
.split_ascii_whitespace()
.map(str::parse)
.collect::<Result<_, _>>()
.ok()
})
.unwrap(),
maps: groups.map(parse_group).collect(),
}
}
}
}
Star 1
What you see here is my solution for star 1 refactored to be re-usable for star 2.
It consists of a generic function star that iterates through all mappings to end up with locations and extracts the minimum.
The initial value, the function to produce the next value and the function to extract the minimum are specific for star_1 and star_2 and passed as parameters.
The step function for star_1 simply checks for every item whether it is contained in any of the mapping ranges. If so, the mapping is applied as an offset, otherwise, the unmodified item is returned.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
fn star<T, S, M>(maps: &[Vec<Map>], seeds: T, mut step: S, mut minimize: M) -> SolT
where
S: FnMut(T, &[Map]) -> T,
M: FnMut(T) -> Option<SolT>,
{
minimize(maps.iter().fold(seeds, |items, map| step(items, map))).unwrap()
}
fn step_1(mut items: Vec<SolT>, map: &[Map]) -> Vec<SolT> {
for item in items.iter_mut() {
if let Some(offset) = map
.iter()
.find(|(_, src_0, len)| (*src_0..*src_0 + len).contains(item))
.map(|(dst_0, src_0, _)| dst_0 - src_0)
{
*item += offset;
}
}
items
}
pub fn star_1(data: &PuzzleData) -> SolT {
star(&data.maps, data.seeds.clone(), step_1, |items| {
items.into_iter().min()
})
}
Star 2
The general structure of the solution for star_2 is the same as the structure for star_1.
The initial value is now ranges, i.e., we need to interpret two consecutive seed values as range start and range length.
The step function finds for every range an overlapping mapping. If there is one, we distinguish the cases when
-
the range is contained in the mapping; then the full range is transformed and added to the result
-
the range is not fully contained in the mapping but overlaps; then the part contained in the mapping is transformed and added to the result, the part not contained in the mapping is processed as additional range
-
the range is not overlapping with any mapping; then it is added to the result as is.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
fn step_2(ranges: Vec<(SolT, SolT)>, map: &[Map]) -> Vec<(SolT, SolT)> {
ranges.iter().fold(Vec::new(), |mut result, &rng| {
let mut rng = Some(rng);
while let Some((rng_0, rng_n)) = rng {
// find a map range that overlaps the current range
// return the transformed contained part and optionally
// a residual untransformed range
let (transformed, residual) = map
.iter()
.map(|&(dst_0, src_0, len)| (dst_0 - src_0, src_0, src_0 + len))
.find(|&(_, src_0, src_n)| {
(src_0..src_n).contains(&rng_0) || (src_0..src_n).contains(&(rng_n - 1))
})
.map(|(dlt, src_0, src_n)| {
match (
(src_0..src_n).contains(&rng_0),
(src_0..src_n).contains(&(rng_n - 1)),
) {
(true, false) => ((rng_0 + dlt, src_n + dlt), Some((src_n, rng_n))),
(false, true) => ((src_0 + dlt, rng_n + dlt), Some((rng_0, src_0))),
_ => ((rng_0 + dlt, rng_n + dlt), None),
}
})
.unwrap_or(((rng_0, rng_n), None));
result.push(transformed);
rng = residual;
}
result
})
}
pub fn star_2(data: &PuzzleData) -> SolT {
star(
&data.maps,
data.seeds
.iter()
.step_by(2)
.zip(data.seeds.iter().skip(1).step_by(2))
.map(|(&from, &len)| (from, from + len))
.collect::<Vec<_>>(),
step_2,
|rng| rng.into_iter().map(|(start, _)| start).min(),
)
}
Tests
Tests are as usual.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"seeds: 79 14 55 13
seed-to-soil map:
50 98 2
52 50 48
soil-to-fertilizer map:
0 15 37
37 52 2
39 0 15
fertilizer-to-water map:
49 53 8
0 11 42
42 0 7
57 7 4
water-to-light map:
88 18 7
18 25 70
light-to-temperature map:
45 77 23
81 45 19
68 64 13
temperature-to-humidity map:
0 69 1
1 0 69
humidity-to-location map:
60 56 37
56 93 4
"#;
#[test]
pub fn test_from() {
let data = PuzzleData::from(CONTENT);
println!("{data:?}");
// check seeds
assert_eq!(vec![79, 14, 55, 13], data.seeds);
}
#[test]
pub fn test_star_1() {
assert_eq!(35, star_1(&CONTENT.into()));
}
#[test]
pub fn test_star_2() {
assert_eq!(46, star_2(&CONTENT.into()));
}
}
Day 6: Wait For It
Rust solution to AoC|2023|6.
Star 1
I went the obvious way and did a linear search for the first star.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
pub fn play_naive((time, dist): (SolT, SolT)) -> SolT {
// distance: (time - b) * b
(0..=time).filter(|&b| (time - b) * b > dist).count() as _
}
pub fn star_1(s: &&str) -> SolT {
#[cfg(feature = "play_math")]
const PLAY: fn((SolT, SolT)) -> SolT = play_math;
#[cfg(all(not(feature = "play_math"), not(feature = "play_1_smart")))]
const PLAY: fn((SolT, SolT)) -> SolT = play_naive;
#[cfg(all(not(feature = "play_math"), feature = "play_1_smart"))]
const PLAY: fn((SolT, SolT)) -> SolT = play_smart;
let mut lines = s.lines().map(|line| {
line.split_ascii_whitespace()
.skip(1)
.map(|value| value.parse::<SolT>().unwrap())
});
lines
.next()
.unwrap()
.zip(lines.next().unwrap())
.map(PLAY)
.product()
}
Star 2
A smarter solution to the same problem: bisection (using the fact that the optimal button press time is known), of course solved with an iterator (who wants to see while loops)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
fn bisect<F: Fn(SolT) -> bool>(bs: (SolT, SolT), test: F) -> (SolT, SolT) {
successors(Some(bs), |&(b_l, b_r)| {
let b = (b_l + b_r) >> 1;
if test(b) {
Some((b_l, b))
} else {
Some((b, b_r))
}
})
.find(|(b_l, b_r)| b_r - b_l <= 1)
.unwrap()
}
pub fn play_smart((time, dist): (SolT, SolT)) -> SolT {
// distance: (time - b) * b
// optimum: time - 2 b = 0 => (time - time >> 1) * (time >> 1)
let b_opt = time >> 1;
let (b_l, _) = bisect((0, b_opt), |b| (time - b) * b > dist);
let (_, b_r) = bisect((b_opt, time), |b| (time - b) * b <= dist);
b_r - b_l - 1
}
pub fn play_math((time, dist): (SolT, SolT)) -> SolT {
// distance: (time - b) * b > dist
// b^2 - time * b + dist = 0
// b = (time +/- sqrt(time^2 - 4 dist)) / 2
let sqrt_d = ((time * time - 4 * dist) as f64).sqrt();
let b1 = (((time as f64) - sqrt_d) / 2.0).floor() as SolT;
let b2 = (((time as f64) + sqrt_d) / 2.0).ceil() as SolT;
b2 - b1 - 1
}
pub fn star_2(s: &&str) -> SolT {
#[cfg(feature = "play_math")]
const PLAY: fn((SolT, SolT)) -> SolT = play_math;
#[cfg(all(not(feature = "play_math"), feature = "play_2_naive"))]
const PLAY: fn((SolT, SolT)) -> SolT = play_naive;
#[cfg(all(not(feature = "play_math"), not(feature = "play_2_naive")))]
const PLAY: fn((SolT, SolT)) -> SolT = play_smart;
let mut values = s.lines().map(|line| {
line.bytes()
.filter(u8::is_ascii_digit)
.fold(0, |val, b| 10 * val + (b - b'0') as SolT)
});
PLAY((values.next().unwrap(), values.next().unwrap()))
}
Later on, I realized that the second part is much more tractable than what I believed and the solution for part 1 is actually good enough. I created features to enable the following variants:
-
cargo run --release --features play_1_smartuses the solution for the second part also for the first part (and uses about the same time) -
cargo run --release --features play_2_naiveuses the solution for the first part also for the second part (and still finishes in a couple of milliseconds)
Benchmarks
And because I was curious on how the code really performs, I also created a Criterion.rs bench for the first time:
1
2
3
4
5
6
7
8
9
10
11
use criterion::{black_box, criterion_group, criterion_main, Criterion};
use mr_kaffee_2023_06::*;
pub fn criterion_benchmark(c: &mut Criterion) {
let data = puzzle().input.into();
c.bench_function("star_1", |b| b.iter(|| star_1(black_box(&data))));
c.bench_function("star_2", |b| b.iter(|| star_2(black_box(&data))));
}
criterion_group!(benches, criterion_benchmark);
criterion_main!(benches);
Tests
Not worth mentioning
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"Time: 7 15 30
Distance: 9 40 200
"#;
#[test]
pub fn test_star_1() {
assert_eq!(288, star_1(&CONTENT));
}
#[test]
pub fn test_star_2() {
assert_eq!(71_503, star_2(&CONTENT));
}
}
Day 7: Camel Cards
Rust solution to AoC|2023|7.
I still prefer Space Cards over Camel Cards ;)
Input
The input is a vector of pairs of cards (as byte array) and bids.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
pub mod input {
use crate::SolT;
#[derive(Debug, PartialEq, Eq)]
pub struct PuzzleData(pub Vec<([u8; 5], SolT)>);
impl<T: AsRef<str>> From<T> for PuzzleData {
fn from(value: T) -> Self {
Self(
value
.as_ref()
.lines()
.filter_map(|line| line.split_once(' '))
.map(|(cards, bid)| {
(
cards.bytes().take(5).enumerate().fold(
[0; 5],
|mut cards, (pos, card)| {
cards[pos] = card;
cards
},
),
bid.parse().unwrap(),
)
})
.collect(),
)
}
}
}
Star 1
I refactored my solution a bit to be usable for both parts. The joker parameter that appears as argument in some of the functions is set to false for the first part.
The idea is to put the hands in a format so that we can sort a vector of hands to get them sorted by rank. This is achieved by representing hands as a pair of a hand type and a cards array.
In the cards array, I cannot use the raw bytes, since that would result in a wrong lexicographically ordering. So I map the raw bytes to an ordinal value using map_cards.
The most tricky part is to determine the type of the hand. The algorithm (implemented in HandType::from(&[u8; 5])) is as follows: count the number of occurrences for every card type in a hand (into an array), extract the two biggest numbers (neglecting the card type) and choose the hand based on those (for part 1, the number of jokers is always 0).
With this, we can sort the hands by rank and calculate the score with a fold.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
pub fn map_cards(cards: &[u8; 5], joker: bool) -> [u8; 5] {
cards.map(|b| match b {
b'A' => 14,
b'K' => 13,
b'Q' => 12,
b'J' if joker => 0,
b'J' => 11,
b'T' => 10,
b => b - b'0',
})
}
#[derive(Debug, PartialEq, Eq, PartialOrd, Ord, Clone, Copy)]
pub enum HandType {
HighCard,
OnePair,
TwoPair,
ThreeOfAKind,
FullHouse,
FourOfAKind,
FiveOfAKind,
}
impl From<&[u8; 5]> for HandType {
fn from(cards: &[u8; 5]) -> Self {
let map = cards.iter().fold([0; 15], |mut map, &card| {
map[card as usize] += 1;
map
});
let jokers = map[0];
let (a, b) = map[2..]
.iter()
.fold((0, 0), |(a, b), &v| match (v > a, v > b) {
(true, _) => (v, a),
(_, true) => (a, v),
_ => (a, b),
});
match (a + jokers, a + b + jokers) {
(5, _) => Self::FiveOfAKind,
(4, _) => Self::FourOfAKind,
(_, 5) => Self::FullHouse,
(3, _) => Self::ThreeOfAKind,
(_, 4) => Self::TwoPair,
(2, _) => Self::OnePair,
_ => Self::HighCard,
}
}
}
pub fn star(PuzzleData(input): &PuzzleData, joker: bool) -> SolT {
let mut hands = input
.iter()
.map(|(cards, bid)| (map_cards(cards, joker), *bid))
.map(|(cards, bid)| ((HandType::from(&cards), cards), bid))
.collect::<Vec<_>>();
hands.sort_unstable();
hands
.iter()
.enumerate()
.map(|(pos, (_, bid))| (pos + 1) * bid)
.sum()
}
pub fn star_1(input: &PuzzleData) -> SolT {
star(input, false)
}
Star 2
In the second part, the symbol J no longer signifies a Jack but a Joker that can stand in for any card but has a lower ordinal number than any other card. This is implemented in map_cards in the line b’J' if joker ⇒ 0 and with the guard conditions in the match statement in HandType::from(&[u8; 5]).
1
2
3
pub fn star_2(input: &PuzzleData) -> SolT {
star(input, true)
}
Tests
One special test today verifies that a hand does not get worse with jokers (on the actual input data)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"32T3K 765
T55J5 684
KK677 28
KTJJT 220
QQQJA 483
"#;
#[test]
pub fn test_input_from() {
let data = PuzzleData::from(CONTENT);
assert_eq!(
PuzzleData(vec![
([b'3', b'2', b'T', b'3', b'K'], 765),
([b'T', b'5', b'5', b'J', b'5'], 684),
([b'K', b'K', b'6', b'7', b'7'], 28),
([b'K', b'T', b'J', b'J', b'T'], 220),
([b'Q', b'Q', b'Q', b'J', b'A'], 483)
]),
data
);
println!("{data:?}");
}
#[test]
pub fn test_star_1() {
assert_eq!(6440, star_1(&CONTENT.into()));
}
#[test]
pub fn test_star_2() {
assert_eq!(5905, star_2(&CONTENT.into()));
}
#[test]
pub fn test_joker() {
let PuzzleData(data) = puzzle().input.into();
for (cards, _) in data.iter() {
assert!(
HandType::from(&map_cards(cards, true)) >= HandType::from(&map_cards(cards, false)),
"Hand got worse with jokers: {:?}",
cards
)
}
}
}
Day 8: Haunted Wasteland
Rust solution to AoC|2023|8.
Input
The input is parsed into a tuple of a byte array representing directions, a vector of tuples consisting of a label and an optional pair of indices to the left and right node representing the map, and a hash map with labels as keys and indices to the vector as value (mainly used to build the vector representation of the map). The vector allows for fast lookups later on, which reduces the overall solution time roughly by a factor of four.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
pub mod input {
use std::collections::{hash_map::Entry, HashMap};
#[derive(Debug, PartialEq, Eq)]
pub struct PuzzleData<'a>(
pub &'a [u8],
pub Vec<(&'a str, Option<(usize, usize)>)>,
pub HashMap<&'a str, usize>,
);
impl<'a, T> From<&'a T> for PuzzleData<'a>
where
T: AsRef<str> + 'a + ?Sized,
{
fn from(s: &'a T) -> Self {
let mut lines = s.as_ref().lines();
let dirs = lines.next().unwrap().as_bytes();
let (map, indices) = lines
.skip(1)
.filter_map(|line| line.split_once(" = "))
.map(|(key, values)| {
(
key,
values
.strip_prefix('(')
.and_then(|values| values.strip_suffix(')'))
.and_then(|values| values.split_once(", "))
.unwrap(),
)
})
.fold(
(
Vec::<(&str, Option<(usize, usize)>)>::new(),
HashMap::<&str, usize>::new(),
),
|(mut map, mut indices), (src, (left, right))| {
let idx_src = find_or_insert(&mut map, &mut indices, src);
let idx_left = find_or_insert(&mut map, &mut indices, left);
let idx_right = find_or_insert(&mut map, &mut indices, right);
map[idx_src].1 = Some((idx_left, idx_right));
(map, indices)
},
);
Self(dirs, map, indices)
}
}
fn find_or_insert<'a>(
map: &mut Vec<(&'a str, Option<(usize, usize)>)>,
indices: &mut HashMap<&'a str, usize>,
label: &'a str,
) -> usize {
match indices.entry(label) {
Entry::Occupied(o) => *o.get(),
Entry::Vacant(v) => {
map.push((label, None));
*(v.insert(map.len() - 1))
}
}
}
}
Star 1
The iterator returned by map_iter navigates the map step by step. The solution just iterates until ZZZ is reached.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
pub fn map_iter<'a>(
dirs: &'a [u8],
map: &'a [(&'a str, Option<(usize, usize)>)],
node: usize,
) -> impl Iterator<Item = (usize, usize)> + 'a {
successors(Some((0, node)), |&(k, node)| {
map[node].1.map(|(left, right)| match dirs[k % dirs.len()] {
b'L' => (k + 1, left),
_ => (k + 1, right),
})
})
}
pub fn star_1(PuzzleData(dirs, map, indices): &PuzzleData) -> SolT {
map_iter(dirs, map, *indices.get("AAA").unwrap())
.find(|(_, node)| map[*node].0 == "ZZZ")
.map(|(steps, _)| steps)
.unwrap()
}
Star 2
The solution is based on a periodicity assumption: Let r be the number of directions given in the puzzle input. Given any start node A, let n_A be the smallest number such that n_A is an integer multiple of r and a target node Z is reached after n_A steps. Then this situation will repeat exactly every n_A steps.
In that case, the solution is the least common multiple (LCM) of all n_A for any possible start node A (for my puzzle, it turned out that any n_A is a prime number multiplied by r, so the LCM calculation could be replaced by simpler multiplications).
The periodicity assumption is essentially a guess, it cannot be derived from the puzzle description. With the feature check-periodicity enabled, the code will verify it (at the cost of doubling the execution time for part 2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
pub fn star_2(PuzzleData(dirs, map, _): &PuzzleData) -> SolT {
map.iter()
.enumerate()
.filter(|(_, (key, _))| key.ends_with('A'))
.map(|(pos, _)| {
let mut it = map_iter(dirs, map, pos)
.step_by(dirs.len()) // only find result that used all dirs
.filter(|(_, node)| map[*node].0.ends_with('Z'));
let (steps_0, node_0) = it.next().unwrap();
if cfg!(feature = "check-periodicity") {
// the solution assumes periodicity, so let's check it
let (steps_1, node_1) = it.next().unwrap();
if steps_1 != 2 * steps_0 || node_1 != node_0 {
panic!("Periodicity assumption not satisfied!");
}
}
steps_0
})
.fold(1, |result, steps| result * steps / gcd(result, steps))
}
Tests
The special "test" test_understand is used to get insight into to puzzle data and verify periodicity. It is supposed to run with the --nocapture option, because printing to stdout is really all it does.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#[cfg(test)]
mod tests {
use std::collections::HashMap;
use super::*;
const CONTENT: &str = r#"LLR
AAA = (BBB, BBB)
BBB = (AAA, ZZZ)
ZZZ = (ZZZ, ZZZ)
"#;
#[test]
pub fn test_from() {
let data = PuzzleData::from(CONTENT);
println!("{data:?}");
assert_eq!(
PuzzleData(
"LLR".as_bytes(),
vec![
("AAA", Some((1, 1))),
("BBB", Some((0, 2))),
("ZZZ", Some((2, 2)))
],
HashMap::from([("AAA", 0), ("BBB", 1), ("ZZZ", 2)])
),
data
);
}
#[test]
pub fn test_star_1() {
assert_eq!(6, star_1(&CONTENT.into()));
}
const CONTENT_2: &str = r#"LR
11A = (11B, XXX)
11B = (XXX, 11Z)
11Z = (11B, XXX)
22A = (22B, XXX)
22B = (22C, 22C)
22C = (22Z, 22Z)
22Z = (22B, 22B)
XXX = (XXX, XXX)
"#;
#[test]
pub fn test_star_2() {
assert_eq!(6, star_2(&CONTENT_2.into()));
}
pub fn do_understand(data: &str, n: usize) {
let PuzzleData(dirs, map, _) = data.into();
for index in map
.iter()
.enumerate()
.filter(|(_, (node, _))| node.ends_with('A'))
.map(|(index, _)| index)
{
println!("Node {}: {}", index, map[index].0);
let mut base = None;
for (pos, node) in map_iter(dirs, &map, index)
.step_by(dirs.len())
.filter(|&(_, x)| map[x].0.ends_with('Z'))
.take(n)
{
let base = *base.get_or_insert(pos);
println!(
" reached {}: {} at step {} = {} * {} + {} = {} * {} + {}",
node,
map[node].0,
pos,
pos / base,
base,
pos % base,
pos / dirs.len(),
dirs.len(),
pos % dirs.len()
);
}
}
}
#[test]
pub fn test_understand() {
println!("\nSample data 2");
println!("=============");
do_understand(CONTENT_2, 4);
println!("\nPuzzle input");
println!("============");
do_understand(puzzle().input, 2);
}
}
Day 9: Mirage Maintenance
Rust solution to AoC|2023|9.
Input
Lines of lists into Vec<Vec<…>>:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
pub mod input {
use crate::SolT;
#[derive(Debug, PartialEq, Eq)]
pub struct PuzzleData(pub Vec<Vec<SolT>>);
impl<T> From<T> for PuzzleData
where
T: AsRef<str>,
{
fn from(s: T) -> Self {
Self(
s.as_ref()
.lines()
.map(|line| {
line.split_ascii_whitespace()
.map(str::parse)
.collect::<Result<_, _>>()
})
.collect::<Result<_, _>>()
.unwrap(),
)
}
}
}
Star 1
I wanted to avoid to allocate a new vector in every iteration step, so I do the processing in place. This results in a successors iterator with side effects on the mutable values vector. Maybe a while loop would be cleaner in that case, but I had to give in to my iterator fetish.
The tail values of all iterations equally contribute to the prediction in a simple sum.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
pub fn extrapolate_back(mut values: Vec<SolT>) -> SolT {
successors(Some((0, values.len())), |&(result, len)| {
if (0..len).all(|k| values[k] == 0) {
None
} else {
let tail = values[len - 1];
for k in 0..len - 1 {
values[k] = values[k + 1] - values[k];
}
Some((result + tail, len - 1))
}
})
.last()
.map(|(result, _)| result)
.unwrap_or(0)
}
pub fn star_1(PuzzleData(values): &PuzzleData) -> SolT {
values.iter().cloned().map(extrapolate_back).sum()
}
Star 2
I was expecting much more complicated. It took a short moment to get the signs right, but essentially, just a duplication of part 1.
The head values of all iterations contribute to the prediction through an alternating sum. The head of the original data contributes positively.
(Alternatively, it is possible to revert the whole list or pseudo-revert it by changing some signs. The main advantage is to avoid code duplication, I guess. I could not measure a significant difference in performance.)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#[cfg(all(not(feature = "reverse"), not(feature = "no-sign")))]
pub fn extrapolate_front(mut values: Vec<SolT>) -> SolT {
successors(Some((0, 1, values.len())), |&(result, sign, len)| {
if len == 0 || (0..len).all(|k| values[k] == 0) {
None
} else {
let head = values[0];
for k in 0..len - 1 {
values[k] = values[k + 1] - values[k];
}
Some((result + sign * head, -sign, len - 1))
}
})
.last()
.map(|(result, _, _)| result)
.unwrap_or(0)
}
#[cfg(all(not(feature = "reverse"), feature = "no-sign"))]
/// variant that inverses the sign in the update steps to get back to
/// a direct sum; this is almost reverting the list of values
pub fn extrapolate_front(mut values: Vec<SolT>) -> SolT {
successors(Some((0, values.len())), |&(result, len)| {
if len == 0 || (0..len).all(|k| values[k] == 0) {
None
} else {
let head = values[0];
for k in 0..len - 1 {
values[k] -= values[k + 1];
}
Some((result + head, len - 1))
}
})
.last()
.map(|(result, _)| result)
.unwrap_or(0)
}
#[cfg(not(feature = "reverse"))]
pub fn star_2(PuzzleData(values): &PuzzleData) -> SolT {
values.iter().cloned().map(extrapolate_front).sum()
}
#[cfg(feature = "reverse")]
/// variant that reverts the list of values and extrapolates at the back
pub fn star_2(PuzzleData(values): &PuzzleData) -> SolT {
values
.iter()
.map(|values| values.iter().rev().copied().collect())
.map(extrapolate_back)
.sum()
}
Tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"0 3 6 9 12 15
1 3 6 10 15 21
10 13 16 21 30 45
"#;
#[test]
pub fn test_from() {
let data = PuzzleData::from(CONTENT);
println!("{data:?}");
assert_eq!(
PuzzleData(vec![
vec![0, 3, 6, 9, 12, 15],
vec![1, 3, 6, 10, 15, 21],
vec![10, 13, 16, 21, 30, 45]
]),
data
);
}
#[test]
pub fn test_star_1() {
assert_eq!(114, star_1(&CONTENT.into()));
}
#[cfg(not(feature = "reverse"))]
#[test]
pub fn test_extrapolate_front() {
let front = extrapolate_front(vec![10, 13, 16, 21, 30, 45]);
assert_eq!(5, front);
}
#[test]
pub fn test_star_2() {
assert_eq!(2, star_2(&CONTENT.into()));
}
}
Day 10: Pipe Maze
Rust solution to AoC|2023|10.
I was a little bit scared when one of the first words I read in the description was "maze"…
Input
I use my utility Grid implementation. A layer of '.' is added around the original grid to avoid special treatment of elements on the boundary.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
pub mod input {
use mr_kaffee_utils::grids::{Grid, MakeGrid};
#[derive(Debug)]
pub struct PuzzleData(pub Grid);
impl<T> From<T> for PuzzleData
where
T: AsRef<[u8]>,
{
fn from(s: T) -> Self {
Self(s.make_grid(Some(b'.')))
}
}
}
Star 1
Walk the loop (since we need to walk the entire loop, there is no advantage in doing a BFS), the max distance is half of the loop length (which is always even). The information which position belongs to the loop is stored in a vector of booleans.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
fn deduce_pipe(grid: &Grid, (col, row): (usize, usize)) -> u8 {
const TO_EAST: [u8; 3] = [b'-', b'J', b'7'];
const TO_NORTH: [u8; 3] = [b'|', b'F', b'7'];
const TO_WEST: [u8; 3] = [b'-', b'F', b'L'];
const TO_SOUTH: [u8; 3] = [b'|', b'L', b'J'];
match (
TO_EAST.contains(&grid[(col + 1, row)]),
TO_NORTH.contains(&grid[(col, row - 1)]),
TO_WEST.contains(&grid[(col - 1, row)]),
TO_SOUTH.contains(&grid[(col, row + 1)]),
) {
(true, true, false, false) => b'L',
(true, false, true, false) => b'-',
(true, false, false, true) => b'F',
(false, true, true, false) => b'J',
(false, true, false, true) => b'|',
(false, false, true, true) => b'7',
_ => panic!(),
}
}
pub fn find_loop(grid: &Grid) -> (SolT, Vec<bool>, u8) {
let start = grid.data().iter().position(|&b| b == b'S').unwrap();
let start_pipe = deduce_pipe(grid, grid.to_col_row(start));
let (len, pipe_loop) = successors(Some((0, start)), |&(prev_idx, cur_idx)| {
let cur = match grid[cur_idx] {
b'S' => start_pipe,
b => b,
};
let (idx_a, idx_b) = match cur {
b'-' => (cur_idx - 1, cur_idx + 1),
b'|' => (cur_idx - grid.width(), cur_idx + grid.width()),
b'J' => (cur_idx - 1, cur_idx - grid.width()),
b'7' => (cur_idx - 1, cur_idx + grid.width()),
b'F' => (cur_idx + 1, cur_idx + grid.width()),
b'L' => (cur_idx + 1, cur_idx - grid.width()),
_ => panic!(),
};
if prev_idx != idx_a && start != idx_a {
Some((cur_idx, idx_a))
} else if prev_idx != idx_b && start != idx_b {
Some((cur_idx, idx_b))
} else {
None
}
})
.fold(
(0, vec![false; grid.len()]),
|(len, mut pipe_loop), (_, idx)| {
pipe_loop[idx] = true;
(len + 1, pipe_loop)
},
);
(len >> 1, pipe_loop, start_pipe)
}
pub fn star_1(PuzzleData(grid): &PuzzleData) -> SolT {
let (mx, _, _) = find_loop(grid);
mx
}
Star 2
The easy part was to figure out that a point is inside the loop if going from that point outwards, we cross the loop an odd number of times.
The tricky part was how to figure out the number of crossings. I decided to always go east. To count the number of crossings, we are only interested in the points that are contained in the pipe, and we can ignore - elements to which we are strictly tangent. Doing so, we just need the current and the previous element to decide whether we crossed the loop. This is the case exactly if the current element is '|' or when the previous and current element are 'L', '7' or 'F', 'J'.
My initial solution checked point by point, adding quite a bit of overhead (the solution is still available by setting feature point-by-point). It is a quite easy modification to count the points inside the loop line by line.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#[cfg(feature = "point-by-point")]
pub fn star_2(PuzzleData(grid): &PuzzleData) -> SolT {
let (_, pipe_loop, start_pipe) = find_loop(grid);
(0..grid.len())
.map(|pos| grid.to_col_row(pos))
.filter(|&(col, row)| !pipe_loop[col + grid.width() * row])
.filter(|&(col, row)| {
// count crossings of pipe
let (cnt, _) = (col + 1..grid.width())
// skip elements not part of pipe
.filter(|&col| pipe_loop[col + grid.width() * row])
// map to elements (substituting 'S')
.map(|col| match grid[(col, row)] {
b'S' => start_pipe,
b => b,
})
// skip purely tangent elements
.filter(|&b| b != b'-')
// count crossings
.fold((0, b'.'), |(cnt, prev), cur| match (prev, cur) {
// "|", "L7", and "FJ" are crossings
(_, b'|') | (b'L', b'7') | (b'F', b'J') => (cnt + 1, cur),
_ => (cnt, cur), // anything else ("LJ", "F7", ...) is not a crossing
});
// odd crossing count is inside
cnt & 1 == 1
})
.count()
}
#[cfg(not(feature = "point-by-point"))]
pub fn star_2(PuzzleData(grid): &PuzzleData) -> SolT {
let (_, pipe_loop, start_pipe) = find_loop(grid);
(0..grid.height())
.map(|row| {
let (cnt, _, _) = (0..grid.width())
.map(
|col| match (pipe_loop[col + grid.width() * row], grid[(col, row)]) {
(true, b'S') => start_pipe,
(true, b) => b,
_ => b'.',
},
)
.filter(|&b| b != b'-')
.fold((0, b'.', false), |(cnt, prev, inside), cur| {
match (inside, prev, cur) {
(true, _, b'.') => (cnt + 1, cur, true),
(_, _, b'|') | (_, b'F', b'J') | (_, b'L', b'7') => (cnt, cur, !inside),
_ => (cnt, cur, inside),
}
});
cnt
})
.sum()
}
Tests
I needed a few test inputs for the second part until I got all the edge cases right. The last missing step, which did actually not fail any of my tests, was to replace 'S' with the pipe type hidden below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"7-F7-
.FJ|7
SJLL7
|F--J
LJ.LJ
"#;
const EXP_STAR_1: SolT = 8;
#[test]
pub fn test_from() {
let data = PuzzleData::from(CONTENT);
assert_eq!(7, data.0.width());
assert_eq!(7, data.0.height());
}
#[test]
pub fn test_star_1() {
assert_eq!(EXP_STAR_1, star_1(&CONTENT.into()));
}
const CONTENT_2: &str = r#"FF7FSF7F7F7F7F7F---7
L|LJ||||||||||||F--J
FL-7LJLJ||||||LJL-77
F--JF--7||LJLJ7F7FJ-
L---JF-JLJ.||-FJLJJ7
|F|F-JF---7F7-L7L|7|
|FFJF7L7F-JF7|JL---7
7-L-JL7||F7|L7F-7F7|
L.L7LFJ|||||FJL7||LJ
L7JLJL-JLJLJL--JLJ.L
"#;
const EXP_2_STAR_2: SolT = 10;
const CONTENT_3: &str = r#"...........
.S-------7.
.|F-----7|.
.||.....||.
.||.....||.
.|L-7.F-J|.
.|..|.|..|.
.L--J.L--J.
...........
"#;
const EXP_3_STAR_2: SolT = 4;
const CONTENT_4: &str = r#".F----7F7F7F7F-7....
.|F--7||||||||FJ....
.||.FJ||||||||L7....
FJL7L7LJLJ||LJ.L-7..
L--J.L7...LJS7F-7L7.
....F-J..F7FJ|L7L7L7
....L7.F7||L7|.L7L7|
.....|FJLJ|FJ|F7|.LJ
....FJL-7.||.||||...
....L---J.LJ.LJLJ...
"#;
const EXP_4_STAR_2: SolT = 8;
#[test]
pub fn test_star_2() {
assert_eq!(EXP_2_STAR_2, star_2(&CONTENT_2.into()));
assert_eq!(EXP_3_STAR_2, star_2(&CONTENT_3.into()));
assert_eq!(EXP_4_STAR_2, star_2(&CONTENT_4.into()));
}
}
Day 11: Cosmic Expansion
Rust solution to AoC|2023|11.
Input
I store the coordinates of each galaxy in a vector and create two more vectors with the galaxy counts in every column/row.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
pub mod input {
#[derive(Debug, PartialEq, Eq, Default)]
pub struct PuzzleData {
pub galaxies: Vec<(usize, usize)>,
pub count_in_cols: Vec<usize>,
pub count_in_rows: Vec<usize>,
}
impl<T> From<T> for PuzzleData
where
T: AsRef<str>,
{
fn from(s: T) -> Self {
s.as_ref()
.lines()
.enumerate()
.fold(PuzzleData::default(), |mut data, (row, line)| {
data.count_in_rows.push(0);
line.bytes().enumerate().filter(|(_, b)| b == &b'#').fold(
data,
|mut data, (col, _)| {
data.galaxies.push((col, row));
data.count_in_cols
.resize(data.count_in_cols.len().max(col + 1), 0);
data.count_in_cols[col] += 1;
data.count_in_rows[row] += 1;
data
},
)
})
}
}
}
Star 1
The basic approach was kind of straight forward. I experimented a bit with possibilities for optimization ending up with computing vectors with the offsets for each column and row that are indexed by the original positions of the galaxies (before expansion of the universe), to calculate the shortest distances in a single pass through all (unordered) pairs of galaxies.
I also experimented a bit with flat_map vs map for the nested iterators. In theory, iter_a.flat_map(|a| iter_b.map(move |b| calc_val(a, b))).sum() should create a bit of overhead compared to iter_a.map(|a| iter_b.map(|b| calc_val(a, b)).sum()).sum(). In practice, the differences were hardly in the range of fluctuations of the overall solution time.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
pub fn calc_offsets(counts: &[usize], expansion: SolT) -> Vec<SolT> {
counts
.iter()
.scan(0, |cum_sum, &cnt| {
let val = Some(*cum_sum);
*cum_sum += if cnt > 0 { 1 } else { expansion };
val
})
.collect()
}
pub fn sum_shortest_path(data: &PuzzleData, expansion: SolT) -> SolT {
let col_offsets = calc_offsets(&data.count_in_cols, expansion);
let row_offsets = calc_offsets(&data.count_in_rows, expansion);
data.galaxies
.iter()
.map(|&(col, row)| (col_offsets[col], row_offsets[row]))
.enumerate()
.map(|(pos, (col_a, row_a))| {
data.galaxies[pos + 1..]
.iter()
.map(|&(col, row)| (col_offsets[col], row_offsets[row]))
.map(|(col_b, row_b)| {
col_b.max(col_a) - col_b.min(col_a) + row_b.max(row_a) - row_b.min(row_a)
})
.sum::<SolT>()
})
.sum()
}
pub fn star_1(data: &PuzzleData) -> SolT {
sum_shortest_path(data, 2)
}
Star 2
Even in my very first version, I did not alter the grid at all but just adjusted coordinates. So the second part was mostly for free (the only catch was to realize that I need to multiply by one million, not add one million).
1
2
3
pub fn star_2(data: &PuzzleData) -> SolT {
sum_shortest_path(data, 1_000_000)
}
Tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"...#......
.......#..
#.........
..........
......#...
.#........
.........#
..........
.......#..
#...#.....
"#;
#[test]
pub fn test_from() {
let data = PuzzleData::from(CONTENT);
println!("{data:?}");
assert_eq!(
PuzzleData {
galaxies: vec![
(3, 0),
(7, 1),
(0, 2),
(6, 4),
(1, 5),
(9, 6),
(7, 8),
(0, 9),
(4, 9)
],
count_in_cols: vec![2, 1, 0, 1, 1, 0, 1, 2, 0, 1],
count_in_rows: vec![1, 1, 1, 0, 1, 1, 1, 0, 1, 2],
},
data
);
}
#[test]
pub fn test_star_1() {
assert_eq!(374, star_1(&CONTENT.into()));
}
#[test]
pub fn test_star_2() {
assert_eq!(1_030, sum_shortest_path(&CONTENT.into(), 10));
assert_eq!(8_410, sum_shortest_path(&CONTENT.into(), 100));
}
}
Day 12: Hot Springs
Rust solution to AoC|2023|12.
Star 1
I implemented a recursive solution in function check_recursive. Take the first group size and find all positions in the operational/damage patterns where it would match. The call check_recursive recursively with the matched part + one operational element stripped from the pattern and the remaining groups.
That’s essentially it for part 1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
pub fn parse_line(line: &str) -> (&[u8], Vec<SolT>) {
line.split_once(' ')
.map(|(data, groups)| {
(
data.as_bytes(),
groups
.split(',')
.map(str::parse)
.collect::<Result<Vec<_>, _>>()
.unwrap(),
)
})
.unwrap()
}
type Cache<'a> = HashMap<(&'a [u8], &'a [SolT]), SolT>;
fn check<'a>(data: &'a [u8], groups: &'a [SolT], cache: &mut Option<Cache<'a>>) -> SolT {
if let Some(&result) = cache.as_ref().and_then(|cache| cache.get(&(data, groups))) {
// return cached result
return result;
}
let result = if groups.is_empty() {
if data.iter().all(|&d| d != b'#') {
1
} else {
0
}
} else {
// minimum elements still required
let min_len = groups.iter().sum::<SolT>() + groups.len() - 1;
// current group (group <= min_len guaranteed)
let group = groups[0];
// result
let mut result = 0;
for pos in 0..(data.len() + 1).saturating_sub(min_len) {
if data[pos..pos + group].iter().all(|&b| b != b'.') {
// next group elements can be damaged
if data.len() == pos + group {
// no more elements
if groups.len() == 1 {
// no more groups
result += 1;
}
} else if data[pos + group] != b'#' {
// next element afterwards can be operational
result += check(&data[pos + group + 1..], &groups[1..], cache);
}
}
if data[pos] == b'#' {
// current element is damaged
break;
}
}
result
};
// cache and return result
cache
.as_mut()
.map(|cache| cache.insert((data, groups), result));
result
}
pub fn star_1(data: &&str) -> SolT {
data.lines()
.map(parse_line)
.map(|(data, groups)| check(data, &groups, &mut None))
.sum()
}
Star 2
The key to solve part 2 in a reasonable time was to add caching of partial results. So if check_recursive is called on something that had been calculated before, recursion is broken and the cached result is returned. I was surprised to see that using one shared cache (across all lines) does not improve performance over individual caches for each line. The initial capacity of the cache has however quite an impact on the performance.
(For part 1, caching is disabled, since caching results in worse runtime)
The solution does not feel very clever…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
const UNFOLDS: usize = 5;
#[cfg(not(feature = "shared-cache"))]
const CACHE_CAPACITY: usize = 1 << 10;
#[cfg(feature = "shared-cache")]
const CACHE_CAPACITY: usize = 1 << 16;
fn make_cache<'a>() -> Option<Cache<'a>> {
Some(Cache::with_capacity(CACHE_CAPACITY))
}
pub fn data_iter(data: &str, unfolds: usize) -> impl Iterator<Item = (Vec<u8>, Vec<SolT>)> + '_ {
data.lines().map(parse_line).map(move |(data, groups)| {
let new_data_len = unfolds * (data.len() + 1) - 1;
let new_groups_len = unfolds * groups.len();
(
data.iter()
.copied()
.chain(once(b'?'))
.cycle()
.take(new_data_len)
.collect::<Vec<_>>(),
groups
.into_iter()
.cycle()
.take(new_groups_len)
.collect::<Vec<_>>(),
)
})
}
#[cfg(not(feature = "shared-cache"))]
pub fn star_2(data: &&str) -> SolT {
data_iter(data, UNFOLDS)
.map(|(data, groups)| check(&data, &groups, &mut make_cache()))
.sum()
}
#[cfg(feature = "shared-cache")]
pub fn star_2(data: &&str) -> SolT {
let mut cache = make_cache();
let data = data_iter(data, UNFOLDS).collect::<Vec<_>>();
data.iter()
.map(|(data, groups)| check(data, groups, &mut cache))
.sum()
}
Tests
Some tests for individual lines proved useful today.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"???.### 1,1,3
.??..??...?##. 1,1,3
?#?#?#?#?#?#?#? 1,3,1,6
????.#...#... 4,1,1
????.######..#####. 1,6,5
?###???????? 3,2,1
"#;
#[test]
pub fn test_check() {
assert_eq!(1, check(".###.##.#...".as_bytes(), &[3, 2, 1], &mut None));
assert_eq!(
0,
check(
".###.##.#...".as_bytes(),
&[3, 2, 2],
&mut Some(Cache::default())
)
);
assert_eq!(
0,
check(".###.##.#...".as_bytes(), &[3, 2, 1, 1], &mut None)
);
assert_eq!(
1,
check(
".###.##....#".as_bytes(),
&[3, 2, 1],
&mut Some(Cache::default())
)
);
const EXP: &[SolT] = &[1, 4, 1, 1, 4, 10];
for (k, (line, &exp)) in CONTENT.lines().zip(EXP.iter()).enumerate() {
let (data, groups) = parse_line(line);
assert_eq!(
exp,
check(data, &groups, &mut (k & 1 == 0).then_some(Cache::default())),
"{}",
line
);
}
}
#[test]
pub fn test_star_1() {
assert_eq!(21, star_1(&CONTENT));
}
#[test]
pub fn test_star_2() {
assert_eq!(525_152, star_2(&CONTENT));
}
}
Day 13: Point of Incidence
Rust solution to AoC|2023|13.
Input
I parse the input by splitting it by consecutive line breaks. This caused quite a bit of headache, because it results in the chunks of input not ending with a line break. So the usual height = len / (width + 1) needs to be replaced by height = (len + 1) / (width + 1). It took I long while for me to find that issue.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
pub mod input {
use crate::SolT;
#[derive(Debug)]
pub struct PuzzleData<'a>(pub Vec<(&'a [u8], SolT)>);
impl<'a, T> From<&'a T> for PuzzleData<'a>
where
T: AsRef<str> + 'a + ?Sized,
{
fn from(s: &'a T) -> Self {
Self(
s.as_ref()
.split("\n\n")
.map(|pattern| {
(
pattern.as_bytes(),
pattern
.bytes()
.position(|b| b == b'\n')
.unwrap_or(pattern.len()),
)
})
.collect(),
)
}
}
}
Star 1
The solution might look a bit over-structured. That is kind of the price for avoiding code duplication (which will become more clear in the second part).
For the first part, we need to solve the same problem essentially twice. Once in the horizontal direction, once in the vertical direction. The find_line method does both. To do so, it takes the argument idx of enum type ToIdx, which converts either (col, row) or (row, col) to a flat index into the array. I did not manage to do this with a closure called from a closure.
The actual algorithm to find the line of symmetry is simple.
The function star accepts the algorithm as an argument f to be re-usable for the second part.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
pub enum ToIdx {
ColRow(SolT),
RowCol(SolT),
}
impl ToIdx {
pub fn idx(&self, x: SolT, y: SolT) -> SolT {
match self {
Self::ColRow(w) => x + y * (w + 1),
Self::RowCol(w) => y + x * (w + 1),
}
}
}
pub fn find_line(pattern: &[u8], d1: SolT, d2: SolT, idx: ToIdx) -> Option<SolT> {
(0..d1 - 1).find(move |&line| {
(0..d2).all(|y| {
(0..=line)
.rev()
.zip(line + 1..d1)
.all(|(x_a, x_b)| pattern[idx.idx(x_a, y)] == pattern[idx.idx(x_b, y)])
})
})
}
pub fn star<F>(data: &[(&[u8], SolT)], f: F) -> SolT
where
F: Fn(&[u8], SolT, SolT, ToIdx) -> Option<SolT>,
{
data.iter()
.filter_map(|&(pattern, w)| {
let h = (pattern.len() + 1) / (w + 1);
f(pattern, w, h, ToIdx::ColRow(w))
.map(|line| line + 1)
.or_else(|| f(pattern, h, w, ToIdx::RowCol(w)).map(|line| (line + 1) * 100))
})
.sum()
}
pub fn star_1(PuzzleData(data): &PuzzleData) -> SolT {
star(data, find_line)
}
Star 2
The second part is solved by adapting the algorithm to not find lines where all elements match, but where there is exactly one that does not match. Against my nature, I implemented this with for loops instead of iterators. The reason is that I can break from the for loop easily as soon as I know that the sum will be larger than one.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
pub fn find_line_with_smudge(pattern: &[u8], d1: SolT, d2: SolT, idx: ToIdx) -> Option<SolT> {
(0..d1 - 1).find(move |&line| {
let mut sum = 0;
for v in (0..d2).map(|y| {
let mut sum = 0;
for v in (0..=line)
.rev()
.zip(line + 1..d1)
.map(|(x_a, x_b)| pattern[idx.idx(x_a, y)] == pattern[idx.idx(x_b, y)])
{
sum += if v { 0 } else { 1 };
if sum > 1 {
break;
}
}
sum
}) {
sum += v;
if sum > 1 {
break;
}
}
sum == 1
})
}
pub fn star_2(PuzzleData(data): &PuzzleData) -> SolT {
star(data, find_line_with_smudge)
}
Tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"#.##..##.
..#.##.#.
##......#
##......#
..#.##.#.
..##..##.
#.#.##.#.
#...##..#
#....#..#
..##..###
#####.##.
#####.##.
..##..###
#....#..#
"#;
#[test]
pub fn test_from() {
let PuzzleData(data) = PuzzleData::from(CONTENT);
assert_eq!(2, data.len());
assert_eq!(9, data[0].1);
assert_eq!(9, data[1].1);
println!("{data:?}");
}
#[test]
pub fn test_find_line_vertical() {
let PuzzleData(data) = PuzzleData::from(CONTENT);
assert_eq!(
vec![Some(4), None],
data.iter()
.map(|&(pattern, w)| find_line(
pattern,
w,
(pattern.len() + 1) / (w + 1),
ToIdx::ColRow(w)
))
.collect::<Vec<_>>()
)
}
#[test]
pub fn test_find_line_horizontal() {
let PuzzleData(data) = PuzzleData::from(CONTENT);
assert_eq!(
vec![None, Some(3)],
data.iter()
.map(|&(pattern, w)| find_line(
pattern,
(pattern.len() + 1) / (w + 1),
w,
ToIdx::RowCol(w)
))
.collect::<Vec<_>>()
);
}
#[test]
pub fn test_star_1() {
assert_eq!(405, star_1(&CONTENT.into()));
}
#[test]
pub fn test_star_2() {
assert_eq!(400, star_2(&CONTENT.into()));
}
}
Day 14: Parabolic Reflector Dish
Rust solution to AoC|2023|14.
Input
Just the plain input plus width and height.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
pub mod input {
#[derive(Debug)]
pub struct PuzzleData<'a>(pub &'a [u8], pub usize, pub usize);
impl<'a, T> From<&'a T> for PuzzleData<'a>
where
T: AsRef<[u8]> + 'a + ?Sized,
{
fn from(s: &'a T) -> Self {
let data = s.as_ref();
let w = data.iter().position(|&b| b == b'\n').unwrap_or(data.len());
let h = (data.len() + 1) / (w + 1);
Self(data, w, h)
}
}
}
Star 1
I just calculated the load without actually modifying the grid.
1
2
3
4
5
6
7
8
9
10
11
12
13
pub fn star_1(&PuzzleData(data, w, h): &PuzzleData) -> usize {
(0..w)
.map(|col| {
(0..h).fold((0, 0), |(load, free), row| {
match data[col + row * (w + 1)] {
b'#' => (load, row + 1),
b'O' => (load + h - free, free + 1),
_ => (load, free),
}
})
})
.fold(0, |sum, (load, _)| sum + load)
}
Star 2
Now, I need to modify the grid - at least I do not have a better idea.
Obviously, this was about finding a shortcut to simulating a billion cycles. I have no idea if there is an analytic way, but given the 'physics' of the problem, there should by periodic cycles after a while.
My first attempt was to check for repetitions in the rock locations themselves. That did not work, because I only compared to the configuration after the first cycle completed, but apparently the inputs are such that it takes a while before we reach the periodic behavior.
Then I just took the loads produced in each direction throughout one cycle and stored them in a vector (the numbers are small enough so that linear search is cheaper than the overhead of a hash map). This solution works independent of the number of initial steps it takes, before repeating cycles start. I might have double-checked that the actual rock locations do repeat as well…
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
pub fn tilt<F: Fn(usize, usize) -> usize>(data: &mut [u8], d1: usize, d2: usize, idx: F) -> usize {
(0..d1)
.map(|x| {
(0..d2).fold((0, 0), |(load, free), y| match data[idx(x, y)] {
b'#' => (load, y + 1),
b'O' => {
data.swap(idx(x, free), idx(x, y));
(load + d2 - free, free + 1)
}
_ => (load, free),
})
})
.fold(0, |sum, (load, _)| sum + load)
}
pub fn cycle(data: &mut [u8], w: usize, h: usize) -> [usize; 4] {
[
tilt(data, w, h, |col, row| col + row * (w + 1)),
tilt(data, h, w, |row, col| col + row * (w + 1)),
tilt(data, w, h, |col, row_inv| col + (h - row_inv - 1) * (w + 1)),
tilt(data, h, w, |row, col_inv| (w - col_inv - 1) + row * (w + 1)),
]
}
pub fn star_2(&PuzzleData(data, w, h): &PuzzleData) -> usize {
let mut data = data.to_owned();
// cycle until repetition is found
let r = (0..)
.scan(Vec::new(), |list, n_1| {
let loads = cycle(&mut data, w, h);
let v = list
.iter()
.position(|prev| prev == &loads)
.map(|n_0| ((1_000_000_000) - (n_1 + 1)) % (n_1 - n_0));
list.push(loads);
Some(v)
})
.flatten()
.next()
.unwrap();
// execute residual cycles
for _ in 0..r {
cycle(&mut data, w, h);
}
// determine load on north (without tilting to north)
(0..w)
.map(|col| {
(0..h)
.filter(|&row| data[col + row * (w + 1)] == b'O')
.map(|row| h - row)
.sum::<usize>()
})
.sum()
}
Tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"O....#....
O.OO#....#
.....##...
OO.#O....O
.O.....O#.
O.#..O.#.#
..O..#O..O
.......O..
#....###..
#OO..#....
"#;
const CONTENT_1: &str = r#".....#....
....#...O#
...OO##...
.OO#......
.....OOO#.
.O#...O#.#
....O#....
......OOOO
#...O###..
#..OO#....
"#;
const CONTENT_2: &str = r#".....#....
....#...O#
.....##...
..O#......
.....OOO#.
.O#...O#.#
....O#...O
.......OOO
#..OO###..
#.OOO#...O
"#;
const CONTENT_3: &str = r#".....#....
....#...O#
.....##...
..O#......
.....OOO#.
.O#...O#.#
....O#...O
.......OOO
#...O###.O
#.OOO#...O
"#;
#[test]
pub fn test_from() {
let PuzzleData(_, w, h) = PuzzleData::from(CONTENT);
assert_eq!(10, w);
assert_eq!(10, h);
}
#[test]
pub fn test_cycle() {
let PuzzleData(data, w, h) = PuzzleData::from(CONTENT);
let mut data = data.to_owned();
cycle(&mut data, w, h);
assert_eq!(String::from_utf8_lossy(&data), CONTENT_1);
cycle(&mut data, w, h);
assert_eq!(String::from_utf8_lossy(&data), CONTENT_2);
cycle(&mut data, w, h);
assert_eq!(String::from_utf8_lossy(&data), CONTENT_3);
}
#[test]
pub fn test_star_1() {
assert_eq!(136, star_1(&CONTENT.into()));
}
#[test]
pub fn test_tilt_north() {
let PuzzleData(data, w, h) = PuzzleData::from(CONTENT);
let mut data = data.to_owned();
assert_eq!(136, tilt(&mut data, w, h, |col, row| col + row * (w + 1)));
}
#[test]
pub fn test_star_2() {
assert_eq!(64, star_2(&CONTENT.into()));
}
}
Day 15: Lens Library
Rust solution to AoC|2023|15.
Star 1
A no-brainer
1
2
3
4
5
6
7
8
pub fn hash(item: &str) -> usize {
item.bytes()
.fold(0, |hash, b| ((hash + (b as usize)) * 17) & 255)
}
pub fn star_1(data: &&str) -> usize {
data.split(',').map(str::trim).map(hash).sum()
}
Star 2
A bit of reading comprehension, mostly.
The input is parsed into pairs of a label and an optional value on the fly.
The vec of boxes is essentially a hash map, each box inside is a bucket of values that produce the same hash. The algorithm to apply for collision resolution is probably something like link::https://en.wikipedia.org/wiki/Hash_table#Separate_chaining[separate chaining], but link::https://rust-unofficial.github.io/too-many-lists/[linked lists] are no fun.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
pub fn star_2(data: &&str) -> usize {
let init_boxes = || {
let mut boxes = Vec::with_capacity(256);
boxes.resize(256, Vec::new());
boxes
};
data.split(',')
.map(str::trim)
.map(|step| {
step.split_once('=')
.map(|(label, value)| (label, Some(value.parse::<usize>().unwrap())))
.or_else(|| step.strip_suffix('-').map(|label| (label, None)))
.unwrap()
})
.fold(init_boxes(), |mut boxes, (label, value)| {
let box_ = &mut boxes[hash(label)];
let idx = box_.iter().position(|(other, _)| other == &label);
match (value, idx) {
(Some(value), Some(idx)) => box_[idx] = (label, value),
(Some(value), _) => box_.push((label, value)),
(_, Some(idx)) => _ = box_.remove(idx),
_ => (),
}
boxes
})
.iter()
.enumerate()
.map(|(box_no, box_)| {
box_.iter()
.enumerate()
.map(|(lens_no, &(_, value))| (box_no + 1) * (lens_no + 1) * value)
.sum::<usize>()
})
.sum()
}
Tests
Only created after the puzzle was solved today.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"rn=1,cm-,qp=3,cm=2,qp-,pc=4,ot=9,ab=5,pc-,pc=6,ot=7"#;
#[test]
pub fn test_star_1() {
assert_eq!(1_320, star_1(&CONTENT));
}
#[test]
pub fn test_star_2() {
assert_eq!(145, star_2(&CONTENT));
}
}
Day 16: The Floor Will Be Lava
Rust solution to AoC|2023|16.
Input
Forward the input data together with grid width and height.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
pub mod input {
#[derive(Debug)]
pub struct PuzzleData<'a>(pub &'a [u8], pub usize, pub usize);
impl<'a, T> From<&'a T> for PuzzleData<'a>
where
T: AsRef<[u8]> + 'a + ?Sized,
{
fn from(s: &'a T) -> Self {
let data = s.as_ref();
let w = data.iter().position(|&b| b == b'\n').unwrap_or(data.len());
let h = (data.len() + 1) / (w + 1);
Self(data, w, h)
}
}
}
Star 1
I implemented a depth first search to let the beam of light traverse the contraption. Breadth first search would have worked just as well, but pushing to and popping from the tail using a Vec is much faster than pushing to one end and popping from the other in a VecDeque.
The state of the search space includes a heading, so a tile is only to be considered seen if there was a beam at the same tile and in the same direction.
Key to performance is: avoid using HashMap, HashSet, VecDeque, …
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
pub const EAST: u8 = 0;
pub const NORTH: u8 = 1;
pub const WEST: u8 = 2;
pub const SOUTH: u8 = 3;
pub const EAST_WEST: u8 = 0;
pub const NORTH_SOUTH: u8 = 1;
#[cfg(feature = "bfs")]
struct Queue<T>(std::collections::VecDeque<T>);
#[cfg(feature = "bfs")]
impl<T> Queue<T> {
fn from<const N: usize>(arr: [T; N]) -> Self {
Self(std::collections::VecDeque::from(arr))
}
fn push(&mut self, value: T) {
self.0.push_back(value);
}
fn pop(&mut self) -> Option<T> {
self.0.pop_front()
}
}
#[cfg(not(feature = "bfs"))]
struct Queue<T>(Vec<T>);
#[cfg(not(feature = "bfs"))]
impl<T> Queue<T> {
fn from<const N: usize>(arr: [T; N]) -> Self {
Self(Vec::from(arr))
}
fn push(&mut self, value: T) {
self.0.push(value);
}
fn pop(&mut self) -> Option<T> {
self.0.pop()
}
}
pub fn simulate_beam(
data: &[u8],
(w, h): (usize, usize),
((col, row), heading): ((usize, usize), u8),
steps: usize,
) -> (Vec<u8>, usize) {
let mut queue = Queue::from([(1, (col, row), heading)]);
let mut seen = vec![0u8; w * h];
seen[col + row * w] |= 1 << heading;
let mut max_steps = 0;
while let Some((cur_steps, (col, row), heading)) = queue.pop() {
max_steps = max_steps.max(cur_steps);
if cur_steps >= steps {
continue;
}
let deltas: &[u8] = match (data[col + row * (w + 1)], heading & 1) {
(b'.', _) | (b'-', EAST_WEST) | (b'|', NORTH_SOUTH) => &[0], // pass-through
(b'-', _) | (b'|', _) => &[1, 3], // split, turn left & right
(b'/', EAST_WEST) | (b'\\', NORTH_SOUTH) => &[1], // turn left
(b'\\', EAST_WEST) | (b'/', NORTH_SOUTH) => &[3], // turn right
_ => panic!(),
};
for delta in deltas {
let heading = (heading + delta) & 3;
let (col, row) = match heading {
EAST => (col + 1, row),
NORTH => (col, row.wrapping_sub(1)),
WEST => (col.wrapping_sub(1), row),
SOUTH => (col, row + 1),
_ => panic!(),
};
if col < w && row < h && (seen[col + row * w] & (1 << heading)) == 0 {
seen[col + row * w] |= 1 << heading;
queue.push((cur_steps + 1, (col, row), heading));
}
}
}
(seen, max_steps)
}
pub fn count_energized(data: &[u8], dims: (usize, usize), beam: ((usize, usize), u8)) -> usize {
simulate_beam(data, dims, beam, usize::MAX)
.0
.into_iter()
.filter(|&v| v > 0)
.count()
}
pub fn star_1(&PuzzleData(data, w, h): &PuzzleData) -> usize {
count_energized(data, (w, h), ((0, 0), EAST))
}
Star 2
I did not have a good idea to implement anything but linear search. And, looking at the time it takes to count energized tiles for one starting position/heading, linear search is good enough.
1
2
3
4
5
6
7
8
9
10
pub fn star_2(&PuzzleData(data, w, h): &PuzzleData) -> usize {
(0..w)
.map(|col| ((col, 0), SOUTH))
.chain((0..h).map(|row| ((w - 1, row), WEST)))
.chain((0..w).map(|col_inv| ((w - col_inv - 1, h - 1), NORTH)))
.chain((0..h).map(|row_inv| ((0, h - row_inv - 1), EAST)))
.map(|start| count_energized(data, (w, h), start))
.max()
.unwrap()
}
Tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#".|...\....
|.-.\.....
.....|-...
........|.
..........
.........\
..../.\\..
.-.-/..|..
.|....-|.\
..//.|....
"#;
#[test]
pub fn test_from() {
let PuzzleData(data, w, h) = PuzzleData::from(CONTENT);
assert_eq!(10, w);
assert_eq!(10, h);
assert_eq!(110, data.len());
}
#[test]
pub fn test_star_1() {
assert_eq!(46, star_1(&CONTENT.into()));
}
#[test]
pub fn test_star_2() {
assert_eq!(51, star_2(&CONTENT.into()));
}
}
Day 17: Clumsy Crucible
Rust solution to AoC|2023|17.
Input
Another grid with width and height.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
pub mod input {
#[derive(Debug)]
pub struct PuzzleData<'a>(pub &'a [u8], pub usize, pub usize);
impl<'a, T> From<&'a T> for PuzzleData<'a>
where
T: AsRef<[u8]> + 'a + ?Sized,
{
fn from(s: &'a T) -> Self {
let data = s.as_ref();
let w = data.iter().position(|b| b == &b'\n').unwrap_or(data.len());
let h = (data.len() + 1) / (w + 1);
Self(data, w, h)
}
}
}
Stars 1 & 2
It is time for Dijkstra and A*!
We need to navigate crucibles on a path that minimizes heat loss. each block of the grid has a heat loss associated to it. The specialty of the problem is that the crucible is constrained in its movement: it needs to advance a minimum number straight before it stops or changes direction and it must not move more than a maximum number of blocks in a straight line before it changes direction.
Obviously, we cannot just take the location on the map as the graph’s nodes. There is at least two ways to model the graph for the problem:
-
Nodes are defined by location, current heading (east, north, west, south), and steps since last change of heading; any node that can be reached by changing direction (if allowed) and moving the minimum number of steps or moving 1 step in the same direction (if allowed) is an adjacent
-
Nodes are defined by location and current heading (horizontal or vertical is enough); any node that can be reached by changing direction and moving any valid number of steps is an adjacent
I came up with the first variant myself and found out about the second variant reading about solution ideas of others.
Since the number of steps since the last change of heading is part of a node’s description in the first variant, there is a single unique predecessor for every node in the graph. This implies that we will never reach a node with any lower cost then the cost assigned to it when we first reached it. We can thus use a simplified version of Dijkstra, where nodes are settled upon expansion, instead of only settling nodes when they are popped from the queue.
The second variant has a much smaller search space (allowing for a Dijkstra implementation without sets or maps), since the number of steps is not included. However, we will in general reach the same node several times and the cost is not guaranteed to be the lowest the first time. As an example, consider the situation below, where the node labeled with the weight (43) (horizontal) is first reached from x with a cost of 43. The node labeled with the weight (7) (horizontal) is also reached from x. Only after the nodes labeled with the weights [11] (vertical), [19] (horizontal), and [23] (vertical) are expanded, the same node is reached a second time with a cost of 35 < 43.
(7) (43)
v v
X 2 2 2 1 9 9 9 9 1 1 1 1 < [23]
1 ^ 1
1 [35] 1
1 1
[11] > 1 1 1 1 1 1 1 1 1 < [19]As a lower bound for the cost to go, I use the minimum cost that would be possible without any constraints on changing direction. This is calculated in loss_bounds. This A* heuristic reduced the runtime quite a bit. The heuristic is on by default. It can be switched off with the feature no-heuristic.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#[cfg(not(feature = "no-heuristic"))]
fn loss_bounds(grid: &[u8], w: usize, h: usize) -> Vec<SolT> {
use std::collections::BinaryHeap;
let target = (w - 1, h - 1);
let mut bounds = vec![SolT::MAX; w * h];
bounds[w * h - 1] = 0;
// queue is a max heap! Need to inverse cost.
let mut queue =
BinaryHeap::from([(SolT::MAX - (grid[(w + 1) * h - 2] - b'0') as SolT, target)]);
while let Some((cost_0, (c0, r0))) = queue.pop() {
for (c1, r1) in D
.map(|(dc, dr)| (c0.wrapping_add_signed(dc), r0.wrapping_add_signed(dr)))
.into_iter()
.filter(|&(c1, r1)| c1 < w && r1 < h)
{
// settle value; this is safe because the cost adder to reach a node
// is the same no matter from which neighbor we reach the node
let r = &mut bounds[c1 + r1 * w];
if *r == SolT::MAX {
*r = SolT::MAX - cost_0;
queue.push((cost_0 - (grid[c1 + r1 * (w + 1)] - b'0') as SolT, (c1, r1)))
}
}
}
bounds
}
#[cfg(not(feature = "no-heuristic"))]
fn loss_bounds_heuristic(grid: &[u8], w: usize, h: usize) -> impl Fn((usize, usize)) -> SolT {
let bounds = loss_bounds(grid, w, h);
move |(col, row)| bounds[col + row * w]
}
#[cfg(feature = "no-heuristic")]
fn loss_bounds_heuristic(_: &[u8], _: usize, _: usize) -> impl Fn((usize, usize)) -> SolT {
|_| 0
}
I implemented both variants. Since the second options requires less run-time, I chose this as default. The first variant can be chosen using feature settle-early.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#[cfg(feature = "settle-early")]
pub fn optimize(grid: &[u8], w: usize, h: usize, s_max: u8, s_min: u8) -> SolT {
use std::collections::{BinaryHeap, HashSet};
use std::iter::successors;
let heuristic = loss_bounds_heuristic(grid, w, h);
let start_cost = heuristic((0, 0));
let starts: [(usize, NodeT); 2] = [
(start_cost, ((0, 0), (0, s_max))),
(start_cost, ((0, 0), (3, s_max))),
];
let target_pos = (w - 1, h - 1);
let mut queue = BinaryHeap::new();
let mut seen = HashSet::new();
for (cost, node) in starts.into_iter() {
queue.push((SolT::MAX - cost, node));
seen.insert(node);
}
#[cfg(feature = "plot")]
let mut parents = HashMap::new();
while let Some((cost_0, ((c0, r0), (hd0, s0)))) = queue.pop() {
if (c0, r0) == target_pos {
#[cfg(feature = "plot")]
println!("{}", to_string(w, h, ((c0, r0), (hd0, s0)), &parents));
return SolT::MAX - cost_0;
}
let dhs: &[u8] = if s0 < s_max { &[0, 1, 3] } else { &[1, 3] };
for (cost_1, node_1) in dhs
.iter()
.map(move |&dh| ((hd0 + dh) & 3, if dh == 0 { s0 } else { 0 }))
.filter_map(|(hd1, s1)| {
// move one step or enough to complete s_min, whatever is more
let to_go = 1.max(s_min - s1.min(s_min));
let (dc, dr) = D[hd1 as usize];
successors(Some((0, c0, r0)), |(weight, c, r)| {
// return Some - summing weights - while in bounds
let (c, r) = (c.wrapping_add_signed(dc), r.wrapping_add_signed(dr));
(c < w && r < h)
.then(|| (weight + (grid[c + r * (w + 1)] - b'0') as SolT, c, r))
})
.nth(to_go as _)
.map(|(weight, c1, r1)| {
(
cost_0 - weight + heuristic((c0, r0)) - heuristic((c1, r1)),
((c1, r1), (hd1, s1 + to_go)),
)
})
})
{
if seen.insert(node_1) {
queue.push((cost_1, node_1));
#[cfg(feature = "plot")]
parents.insert(node_1, ((c0, r0), (hd0, s0)));
}
}
}
panic!("No solution found.")
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#[cfg(not(feature = "settle-early"))]
pub fn optimize(grid: &[u8], w: usize, h: usize, s_max: u8, s_min: u8) -> SolT {
use std::collections::BinaryHeap;
use std::iter::successors;
let heuristic = &loss_bounds_heuristic(grid, w, h);
let start_cost = SolT::MAX - heuristic((0, 0));
let starts: [(usize, NodeT); 2] = [(start_cost, ((0, 0), 0)), (start_cost, ((0, 0), 1))];
let target_pos = (w - 1, h - 1);
let mut queue = BinaryHeap::new();
let mut settled = vec![0u8; w * h];
let mut costs = vec![0; w * h * 2];
for (cost, ((c, r), o)) in starts.into_iter() {
queue.push((cost, ((c, r), o)));
costs[c + r * w + (o as usize) * w * h] = cost;
}
#[cfg(feature = "plot")]
let mut parents = HashMap::new();
while let Some((cost_0, ((c0, r0), o0))) = queue.pop() {
if (c0, r0) == target_pos {
#[cfg(feature = "plot")]
println!("{}", to_string(w, h, ((c0, r0), o0), &settled, &parents));
return SolT::MAX - cost_0;
}
if settled[c0 + r0 * w] & (1 << o0) == 0 {
settled[c0 + r0 * w] |= 1 << o0;
} else {
continue;
}
for (cost_1, ((c1, r1), o1)) in [1, 3]
.iter()
.map(move |&dh| D[(o0 as usize + dh) & 3])
.flat_map(|(dc, dr)| {
successors(Some((0, c0, r0)), move |(weight, c, r)| {
let (c, r) = (c.wrapping_add_signed(dc), r.wrapping_add_signed(dr));
(c < w && r < h)
.then(|| (weight + (grid[c + r * (w + 1)] - b'0') as SolT, c, r))
})
.take(s_max as usize + 1)
.skip(1.max(s_min as _))
.map(move |(weight, c1, r1)| {
(
cost_0 - weight + heuristic((c0, r0)) - heuristic((c1, r1)),
((c1, r1), !o0 & 1),
)
})
})
.filter(|(_, ((r1, c1), o1))| settled[r1 + c1 * w] & (1 << o1) == 0)
{
let cost_1_prev = &mut costs[c1 + r1 * w + (o1 as usize) * w * h];
if cost_1 > *cost_1_prev {
*cost_1_prev = cost_1;
queue.push((cost_1, ((c1, r1), o1)));
#[cfg(feature = "plot")]
parents.insert(((c1, r1), o1), ((c0, r0), o0));
}
}
}
panic!("No solution found.")
}
Tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"2413432311323
3215453535623
3255245654254
3446585845452
4546657867536
1438598798454
4457876987766
3637877979653
4654967986887
4564679986453
1224686865563
2546548887735
4322674655533
"#;
const CONTENT_2: &str = r#"111111111111
999999999991
999999999991
999999999991
999999999991
"#;
#[test]
pub fn test_from() {
let PuzzleData(grid, w, h) = PuzzleData::from(CONTENT);
assert_eq!(13, w);
assert_eq!(13, h);
assert_eq!(13 * 14, grid.len());
}
#[test]
pub fn test_star_1() {
assert_eq!(102, star_1(&CONTENT.into()));
}
#[test]
pub fn test_star_2() {
assert_eq!(94, star_2(&CONTENT.into()));
assert_eq!(71, star_2(&CONTENT_2.into()));
}
#[cfg(not(feature = "no-heuristic"))]
#[test]
pub fn test_loss_bounds() {
let PuzzleData(grid, w, h) = CONTENT_2.into();
let bounds = loss_bounds(grid, w, h);
for row in 0..h {
for col in 0..w {
print!("{:>3}", bounds[col + row * w]);
}
println!();
}
let exp = [
[15, 14, 13, 12, 11, 10, 9, 8, 7, 6, 5, 4],
[16, 15, 14, 13, 12, 11, 10, 9, 8, 7, 4, 3],
[25, 24, 23, 22, 21, 20, 19, 18, 17, 12, 3, 2],
[34, 33, 32, 31, 30, 29, 28, 27, 20, 11, 2, 1],
[43, 42, 41, 40, 39, 38, 37, 28, 19, 10, 1, 0],
]
.concat();
assert_eq!(exp, bounds);
}
}
Images
Part 1 with and without heuristic

Part 2 with and without heuristic


(light blue: settled, medium blue: reached, dark blue: not reached)
Day 18: Lavaduct Lagoon
Rust solution to AoC|2023|18.
Star 1
On 10, we already calculated the surface enclosed in a polygon. Back then I scanned the complete grid line by line. Today, it is time for the Shoelace formula. I quickly looked at it already when solving day 10.
The only part that requires some thinking is how to account for the fact that the coordinates represent lines of width 1. The shoelace formula gives the area, that we would get if we had zero-width lines centered in the actual lines. So we have to add half of the number of elements on the perimeter. For the corners, if we walk across the perimeter clockwise, a right turn will contribute three quarters of a unit while a left turn will contribute one quarter of a unit. Since we end up at the origin, there must be a right turn for every left turn plus an additional four right turns. Hence, I need to add one unit.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
pub fn shoelace<F>(data: F) -> SolT
where
F: Iterator<Item = (u8, SolT)>,
{
let (_, s, p) = data.fold(((0, 0), 0, 0), |((x0, y0), s, p), (d, len)| {
let (x1, y1) = match d {
0 => (x0 + len, y0),
1 => (x0, y0 + len),
2 => (x0 - len, y0),
3 => (x0, y0 - len),
_ => unreachable!(),
};
(
(x1, y1),
s + (y0 + y1) * (x0 - x1),
p + x0.max(x1) - x0.min(x1) + y0.max(y1) - y0.min(y1),
)
});
s / 2 + p / 2 + 1
}
pub fn star_1(data: &&str) -> SolT {
shoelace(data.lines().map(|line| {
let mut parts = line.split_ascii_whitespace();
(
match parts.next().unwrap() {
"R" => 0,
"D" => 1,
"L" => 2,
"U" => 3,
d => panic!("Illegal direction: {}", d),
},
parts.next().unwrap().parse().unwrap(),
)
}))
}
Star 2
Same as star 1.
1
2
3
4
5
6
7
8
9
pub fn star_2(data: &&str) -> SolT {
shoelace(data.lines().map(|line| {
line.split_ascii_whitespace()
.nth(2)
.and_then(|code| SolT::from_str_radix(&code[2..code.len() - 1], 16).ok())
.map(|code| ((code & 0xf) as _, code >> 4))
.unwrap()
}))
}
Tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"R 6 (#70c710)
D 5 (#0dc571)
L 2 (#5713f0)
D 2 (#d2c081)
R 2 (#59c680)
D 2 (#411b91)
L 5 (#8ceee2)
U 2 (#caa173)
L 1 (#1b58a2)
U 2 (#caa171)
R 2 (#7807d2)
U 3 (#a77fa3)
L 2 (#015232)
U 2 (#7a21e3)
"#;
#[test]
pub fn test_star_1() {
assert_eq!(62, star_1(&CONTENT));
}
#[test]
pub fn test_star_2() {
assert_eq!(952_408_144_115, star_2(&CONTENT));
}
}
Day 19: Aplenty
Rust solution to AoC|2023|19.
Input
Input parsing was a bit tedious today. Maybe regex would have worked faster here, but I still only use standard library.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
pub mod input {
use std::{cmp::Ordering, collections::HashMap};
pub type ValT = usize;
pub type RuleT<'a> = (Option<(usize, Ordering, ValT)>, &'a str);
pub type PartT = [ValT; 4];
#[derive(Debug)]
pub struct PuzzleData<'a>(pub HashMap<&'a str, Vec<RuleT<'a>>>, pub Vec<PartT>);
fn parse_rule(rule: &'_ str) -> RuleT<'_> {
rule.split_once(':')
.map(|(cond, target)| {
(
Some((
match cond.as_bytes()[0] {
b'x' => 0,
b'm' => 1,
b'a' => 2,
b's' => 3,
b => panic!("Bad symbol: '{}'", b as char),
},
match cond.as_bytes()[1] {
b'>' => Ordering::Greater,
b'<' => Ordering::Less,
b => panic!("Bad symbol: '{}'", b as char),
},
cond[2..].parse().unwrap(),
)),
target,
)
})
.unwrap_or((None, rule))
}
fn parse_workflows(workflow: &'_ str) -> HashMap<&'_ str, Vec<RuleT<'_>>> {
workflow
.lines()
.map(|line| {
line.split_once('{')
.and_then(|(label, rules)| rules.strip_suffix('}').map(|rules| (label, rules)))
.unwrap()
})
.map(|(label, rules)| (label, rules.split(',').map(parse_rule).collect()))
.collect()
}
fn parse_parts(parts: &str) -> Vec<PartT> {
parts
.lines()
.map(|part| {
let mut values = part
.trim_matches::<&[char]>(&['{', '}'])
.split(',')
.map(|n| n[2..].parse().unwrap());
[
values.next().unwrap(),
values.next().unwrap(),
values.next().unwrap(),
values.next().unwrap(),
]
})
.collect()
}
impl<'a, T> From<&'a T> for PuzzleData<'a>
where
T: AsRef<str> + 'a + ?Sized,
{
fn from(s: &'a T) -> Self {
s.as_ref()
.split_once("\n\n")
.map(|(workflows, parts)| Self(parse_workflows(workflows), parse_parts(parts)))
.unwrap()
}
}
}
Star 1
Just recurse through the workflows until a part is accepted or rejected. Recursion is done using a successors iterator.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
pub fn star_1(PuzzleData(workflows, parts): &PuzzleData) -> SolT {
parts
.iter()
.filter(|part| {
Some("A")
== successors(Some("in"), |&target| {
workflows.get(target).and_then(|workflow| {
workflow
.iter()
.find(|(cond, _)| {
cond.map(|(idx, ord, val)| part[idx].cmp(&val) == ord)
.unwrap_or(true)
})
.map(|&(_, target)| target)
})
})
.last()
})
.map(|part| part.iter().sum::<SolT>())
.sum()
}
Star 2
Divide and conquer!
Any rule splits the allowed ranges in one part which matches the rule and another part which does not (both are possibly empty). These two parts are then handled separately. The part with matches by recursing to the target workflow of the rule, the part which does not match by checking the next rule in the workflow.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
pub fn star_2_rec(
workflows: &HashMap<&str, Vec<RuleT>>,
target: &str,
mut v_min: PartT,
mut v_max: PartT,
) -> SolT {
match target {
"A" => {
return (0..4)
.map(|idx| (v_max[idx] - v_min[idx]) as SolT)
.product()
}
"R" => return 0,
_ => (),
}
let mut count = 0;
for (rule, next) in workflows.get(target).unwrap() {
match rule
.map(|(idx, ord, val)| {
(
idx,
val,
v_min[idx].cmp(&val) == ord,
(v_max[idx] - 1).cmp(&val) == ord,
)
})
.unwrap_or((0, 0, true, true))
{
(_, _, false, false) => (), // rule does not match at all -> check next rule
(_, _, true, true) => {
// rule fully matches -> recurse and stop checking further rules here
return count + star_2_rec(workflows, next, v_min, v_max);
}
(idx, val, true, false) => {
// rule matches for values_min_match[idx]..val -> recurse
let (v_min_rec, mut v_max_rec) = (v_min, v_max);
v_max_rec[idx] = val;
count += star_2_rec(workflows, next, v_min_rec, v_max_rec);
// rule does not match for val..values_max[idx] -> check next rule
v_min[idx] = val;
}
(idx, val, false, true) => {
// rule matches for val + 1..values_max_match[idx] -> recurse
let (mut v_min_rec, v_max_rec) = (v_min, v_max);
v_min_rec[idx] = val + 1;
count += star_2_rec(workflows, next, v_min_rec, v_max_rec);
// rule does not match for values_min[idx]..val + 1 -> check next rule
v_max[idx] = val + 1;
}
}
}
unreachable!("Eventually everything shall match")
}
pub fn star_2(PuzzleData(workflows, _): &PuzzleData) -> SolT {
star_2_rec(workflows, "in", [1; 4], [4001; 4])
}
Tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"px{a<2006:qkq,m>2090:A,rfg}
pv{a>1716:R,A}
lnx{m>1548:A,A}
rfg{s<537:gd,x>2440:R,A}
qs{s>3448:A,lnx}
qkq{x<1416:A,crn}
crn{x>2662:A,R}
in{s<1351:px,qqz}
qqz{s>2770:qs,m<1801:hdj,R}
gd{a>3333:R,R}
hdj{m>838:A,pv}
{x=787,m=2655,a=1222,s=2876}
{x=1679,m=44,a=2067,s=496}
{x=2036,m=264,a=79,s=2244}
{x=2461,m=1339,a=466,s=291}
{x=2127,m=1623,a=2188,s=1013}
"#;
#[test]
pub fn test_from() {
let data = PuzzleData::from(CONTENT);
println!("{data:?}");
}
#[test]
pub fn test_star_1() {
assert_eq!(19_114, star_1(&CONTENT.into()));
}
#[test]
pub fn test_star_2() {
assert_eq!(167_409_079_868_000, star_2(&CONTENT.into()));
}
}
Day 20: Pulse Propagation
Rust solution to AoC|2023|20.
Input
Reading and understanding the puzzle description was a bit of a challenge today.
The puzzle contains nodes that have a type (plain, flip-flop, conjunction) and an identifier. Each node has zero to many target nodes it sends to.
To avoid expensive lookups later on, I assign a unique id to each node, which can be used directly as index into vectors.
The input is modeled as a vector of vectors for the targets, a vector of types (u8) and the ids of the broadcaster and, if present, the rx node (needed for part 2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
pub mod input {
#[derive(Debug, PartialEq, Eq)]
pub struct PuzzleData {
pub bc: usize,
pub rx: Option<usize>,
pub targets: Vec<Vec<usize>>,
pub types: Vec<u8>,
}
fn get_id<'a>(nodes: &mut Vec<&'a str>, node: &'a str) -> usize {
let id = nodes.iter().position(|&n| n == node).unwrap_or(nodes.len());
if id == nodes.len() {
nodes.push(node);
}
id
}
impl<T> From<&T> for PuzzleData
where
T: AsRef<str> + ?Sized,
{
fn from(s: &T) -> Self {
let mut nodes = Vec::new();
let mut targets = Vec::new();
let mut types = Vec::new();
for line in s.as_ref().lines() {
let (source, targets_part) = line.split_once(" -> ").unwrap();
let (source_type, source) = match source.as_bytes()[0] {
b'%' => (b'%', &source[1..]),
b'&' => (b'&', &source[1..]),
b if b.is_ascii_alphabetic() => (0, source),
_ => panic!(),
};
let source_id = get_id(&mut nodes, source);
let target_ids = targets_part
.split(", ")
.map(|target| get_id(&mut nodes, target))
.collect::<Vec<_>>();
targets.resize(nodes.len(), Vec::default());
targets[source_id] = target_ids;
types.resize(nodes.len(), 0);
types[source_id] = source_type;
}
let bc = nodes
.iter()
.position(|&name| name == "broadcaster")
.unwrap();
let rx = nodes.iter().position(|&name| name == "rx");
Self {
bc,
rx,
targets,
types,
}
}
}
}
Star 1
Nodes may have memory assigned to them. Flip-flops have a single bit, conjunctions have multiple bits, and plain nodes do not have any memory. For conjunction nodes, each bit of memory is reserved to receive data from one specific source.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#[derive(Clone, PartialEq, Eq)]
pub enum Mem {
Plain,
FlipFlop(bool),
Conjunction(Vec<(usize, bool)>),
}
pub fn dump_memory(mems: &[Mem]) -> (u128, u128) {
mems.iter().fold((0, 0), |(dump, mask), mem| match mem {
Mem::Plain => (dump, mask),
Mem::FlipFlop(val) => (dump << 1 | *val as u128, mask << 1 | 1),
Mem::Conjunction(values) => values.iter().fold((dump, mask), |(dump, mask), (_, val)| {
(dump << 1 | *val as u128, mask << 1 | 1)
}),
})
}
pub fn init(targets: &[Vec<usize>], types: &[u8]) -> Vec<Mem> {
let mut memories = types
.iter()
.map(|&t| match t {
0 => Mem::Plain,
b'&' => Mem::Conjunction(Vec::new()),
b'%' => Mem::FlipFlop(false),
_ => panic!(),
})
.collect::<Vec<_>>();
for (k, targets) in targets.iter().enumerate() {
for &target in targets {
if let Mem::Conjunction(ref mut vec) = &mut memories[target] {
vec.push((k, false));
}
}
}
memories
}
To solve the first part, I first implemented a function that simulates a single button press. It accepts a callback to do something upon transmissions. Packets are pushed in a FIFO queue to make sure the order is preserved.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
pub fn press_button<F>(memories: &mut [Mem], bc: usize, targets: &[Vec<usize>], mut callback: F)
where
F: FnMut(usize, usize, bool),
{
let mut queue = VecDeque::new();
for &target in &targets[bc] {
queue.push_back((target, bc, false));
}
while let Some((target, source, value)) = queue.pop_front() {
callback(target, source, value);
match &mut memories[target] {
Mem::FlipFlop(ref mut mem) if !value => {
*mem = !*mem;
for &t in &targets[target] {
queue.push_back((t, target, *mem));
}
}
Mem::Conjunction(ref mut mems) => {
let (_, mem) = mems.iter_mut().find(|(id, _)| *id == source).unwrap();
*mem = value;
let upd = !mems.iter().all(|(_, v)| *v);
for &t in &targets[target] {
queue.push_back((t, target, upd));
}
}
_ => (),
}
}
}
I then created a SendCounter struct, which provides the callback and does the counting, and that’s basically it.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#[derive(Debug, Default, PartialEq, Eq)]
struct SendCounter(usize, usize);
impl SendCounter {
fn callback(&mut self) -> impl FnMut(usize, usize, bool) + '_ {
|_, _, value| self.count(value)
}
fn count(&mut self, value: bool) {
if value {
self.0 += 1
} else {
self.1 += 1
}
}
fn get(&self) -> usize {
self.0 * self.1
}
}
pub fn star_1(
PuzzleData {
bc, targets, types, ..
}: &PuzzleData,
) -> usize {
let mut mem = init(targets, types);
let mut counter = SendCounter::default();
for _ in 0..1_000 {
counter.count(false); // button press
press_button(&mut mem, *bc, targets, counter.callback());
}
counter.get()
}
Star 2
I am not sure how much I like that second part.
It is one of the challenges, where we need to exploit properties of the puzzle input, that the description does not disclose.
It turned out quite quickly, that there is no periodicity that can be reasonable exploited (obviously there is periodicity, since there is a finite number of states, 91 bits in my case)
After playing around a while, I realized that there is a single node that sends to rx, which is a conjunction. All nodes that send to this conjunction turn out to send high with a periodicity of some large prime number. So the answer is the product of those prime numbers.
There is again a struct, Sources, which is used to determine the number of steps it takes to reach all nodes that send to the single source node of rx.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
struct Sources {
values: Vec<Option<usize>>,
source: usize,
source_sources: Vec<usize>,
buttons: usize,
}
pub fn find_sources(targets: &[Vec<usize>], target: usize) -> Vec<usize> {
targets
.iter()
.enumerate()
.filter(|(_, targets)| targets.contains(&target))
.map(|(pos, _)| pos)
.collect()
}
impl Sources {
fn create(targets: &[Vec<usize>], rx: usize) -> Self {
let sources = find_sources(targets, rx);
assert_eq!(1, sources.len());
let source = sources[0];
let source_sources = find_sources(targets, source);
let values = vec![None; source_sources.len()];
Self {
values,
source,
source_sources,
buttons: 0,
}
}
fn callback(&mut self) -> impl FnMut(usize, usize, bool) + '_ {
|target, source, value| {
if target == self.source && value {
let id = self
.source_sources
.iter()
.position(|&id| id == source)
.unwrap();
if self.values[id].is_none() {
self.values[id] = Some(self.buttons);
}
}
}
}
fn button(&mut self) {
self.buttons += 1;
}
fn done(&self) -> bool {
self.values.iter().all(|v| v.is_some())
}
fn get(&mut self) -> usize {
self.values.iter().flatten().product()
}
}
pub fn star_2(
PuzzleData {
bc,
rx,
targets,
types,
}: &PuzzleData,
) -> usize {
let mut memories = init(targets, types);
let mut sources = Sources::create(targets, rx.unwrap());
while !sources.done() {
sources.button();
press_button(&mut memories, *bc, targets, sources.callback());
}
sources.get()
}
Tests
Today was more a day for exploratory testing (aka run, print debug statements, run again, try this and that, find patterns, …). The dump_memory function is a left-over from this.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#[cfg(test)]
mod tests {
use super::*;
const CONTENT_1: &str = r#"broadcaster -> a, b, c
%a -> b
%b -> c
%c -> inv
&inv -> a
"#;
const CONTENT_2: &str = r#"broadcaster -> a
%a -> inv, con
&inv -> b
%b -> con
&con -> output
"#;
#[test]
pub fn test_from() {
let data = PuzzleData::from(CONTENT_1);
// "broadcaster", "a", "b", "c", "inv"
let exp = PuzzleData {
bc: 0,
rx: None,
targets: vec![vec![1, 2, 3], vec![2], vec![3], vec![4], vec![1]],
types: vec![0, b'%', b'%', b'%', b'&'],
};
println!("{data:?}");
assert_eq!(exp, data);
let data = PuzzleData::from(CONTENT_2);
// "broadcaster", "a", "inv", "con", "b", "output"
let exp = PuzzleData {
bc: 0,
rx: None,
targets: vec![vec![1], vec![2, 3], vec![4], vec![5], vec![3], vec![]],
types: vec![0, b'%', b'&', b'&', b'%', 0],
};
println!("{data:?}");
assert_eq!(exp, data);
}
#[test]
pub fn test_star_1() {
assert_eq!(32_000_000, star_1(&CONTENT_1.into()));
assert_eq!(11_687_500, star_1(&CONTENT_2.into()));
}
#[test]
pub fn test_press_button_with_send_counter() {
let PuzzleData {
bc,
rx: _,
targets,
types,
} = CONTENT_2.into();
let mut mem = init(&targets, &types);
let mut counter = SendCounter::default();
press_button(&mut mem, bc, &targets, counter.callback());
assert_eq!(SendCounter(4, 3), counter);
press_button(&mut mem, bc, &targets, counter.callback());
assert_eq!(SendCounter(4 + 2, 3 + 3), counter);
}
#[test]
pub fn test_dump_memory() {
let PuzzleData {
bc: _,
rx: _,
targets,
types,
} = CONTENT_1.into();
let mem = init(&targets, &types);
assert_eq!((0, 0xf), dump_memory(&mem));
}
}
Day 21: Step Counter
Rust solution to AoC|2023|21.
The solution got somehow complicated today.
The solution uses the fact that there are no rocks on the perimeter of a garden tile. This results in the 'diagonal tiles' to repeat themselves, all tiles above and to the right of the center tile have identical costs modulo an offset. The same is true for the north-west, south-west and south-east tiles.
The tiles in a straight line from the center tile also happen to repeat (after a few initial tiles). This allows to replace most of the counting by direct calculations.
Here is the not so nice looking solution:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
pub type Steps = u32;
#[derive(Debug, PartialEq, Eq, PartialOrd, Ord, Clone, Copy)]
pub enum Heading {
East = 0,
North = 1,
West = 2,
South = 3,
}
#[derive(Debug, PartialEq, Eq, PartialOrd, Ord)]
pub struct Boundary {
offset: usize,
heading: Heading,
data: Vec<Steps>,
}
impl Boundary {
pub fn from_matrix(
data: &[Steps],
w: usize,
h: usize,
heading: Heading,
offset: usize,
) -> Self {
let mut data: Vec<_> = match heading {
Heading::East => (0..h)
.map(|row_inv| data[w - 1 + (h - 1 - row_inv) * w])
.collect(),
Heading::North => (0..w).map(|col_inv| data[w - 1 - col_inv]).collect(),
Heading::West => (0..h).map(|row| data[row * w]).collect(),
Heading::South => (0..w).map(|col| data[col + (h - 1) * w]).collect(),
};
let min_cost = *data.iter().min().unwrap();
let offset = if min_cost == Steps::MAX {
usize::MAX
} else {
data.iter_mut()
.filter(|d| **d != Steps::MAX)
.for_each(|d| *d -= min_cost);
offset + min_cost as usize
};
Self {
data,
heading,
offset,
}
}
}
#[derive(Debug, PartialEq, Eq)]
pub struct Grid<'a> {
pub(crate) data: &'a [u8],
pub(crate) w: usize,
pub(crate) h: usize,
}
mod grid {
use super::Steps;
pub(crate) fn cost_counts(costs: &[Steps]) -> Vec<usize> {
costs.iter().filter(|&&cost| cost != Steps::MAX).fold(
Vec::<usize>::new(),
|mut counts, &cost| {
counts.resize(counts.len().max(cost as usize + 1), 0);
counts[cost as usize] += 1;
counts
},
)
}
pub(crate) fn count_reachable(costs: &[Steps], offset: usize, steps: usize) -> usize {
costs
.iter()
.map(|&cost| offset + cost as usize)
.filter(|&cost| cost <= steps && cost & 1 == steps & 1)
.count()
}
}
impl<'a, T> From<&'a T> for Grid<'a>
where
T: AsRef<[u8]> + 'a + ?Sized,
{
fn from(value: &'a T) -> Self {
let data = value.as_ref();
let w = data.iter().position(|&b| b == b'\n').unwrap_or(data.len());
let h = (data.len() + 1) / (w + 1);
Self { data, w, h }
}
}
impl Grid<'_> {
pub fn get_start(&self) -> (usize, usize) {
self.data
.iter()
.position(|&b| b == b'S')
.map(|p| (p % (self.w + 1), p / (self.w + 1)))
.unwrap()
}
pub fn reachable_in_steps(&self, steps: usize) -> usize {
assert!(self.w == self.h);
let (mut total_count, boundaries) = self.center_tile_boundaries(steps);
for boundary in boundaries
.as_ref()
.iter()
.filter(|boundary| boundary.offset != usize::MAX && boundary.data[0] != Steps::MAX)
{
let offset = boundary.offset + boundary.data[0] as usize + 1;
let data = (0..boundary.data.len() as Steps).rev().collect();
let boundary = Boundary {
data,
offset,
heading: boundary.heading,
};
let (_, costs) = self.next_boundary(&boundary, usize::MAX);
let cost_counts = grid::cost_counts(&costs);
// fits if offset + (s - 1) * self.w + max_steps <= steps
// (s - 1) * self.w <= (steps - offset - max_steps)
let n = (steps + self.w).saturating_sub(offset + cost_counts.len() - 1) / self.w;
// short cut as long as max_step fits
if n > 0 {
let cost_counts_even = cost_counts.iter().step_by(2).skip(1).sum::<usize>();
let cost_counts_odd = cost_counts.iter().skip(1).step_by(2).sum::<usize>();
// sum of even numbers from 1 to n
let sum_even = 2 * (n / 2 + 1) * (n / 2) / 2;
// sum of odd numbers from 1 to n
let sum_odd = 2 * ((n + 1) / 2 + 1) * ((n + 1) / 2) / 2 - (n + 1) / 2;
total_count += if (steps - offset) & 1 == 0 {
sum_odd * cost_counts_even + sum_even * cost_counts_odd
} else {
sum_odd * cost_counts_odd + sum_even * cost_counts_even
};
}
// do the counting for the remaining tiles
for s in n + 1.. {
let off = offset + (s - 1) * self.w;
let count = grid::count_reachable(&costs, off, steps);
total_count += s * count;
if count == 0 {
break;
}
}
}
for boundary in boundaries
.into_iter()
.filter(|boundary| boundary.offset != usize::MAX)
{
// find steady state
let mut cur = boundary;
let steady_state = loop {
let (next, costs) = self.next_boundary(&cur, steps);
total_count += grid::count_reachable(&costs, cur.offset, steps);
let Some(next) = next else { break None };
if cur.data == next.data {
break Some((next, costs));
}
cur = next;
};
let Some((boundary, costs)) = steady_state else {
continue;
};
let offset = boundary.offset;
let cost_counts = grid::cost_counts(&costs);
// fits if offset + (s - 1) * self.w + max_steps <= steps
// (s - 1) * self.w <= (steps - offset - max_steps)
let n = (steps + self.w).saturating_sub(offset + cost_counts.len() - 1) / self.w;
if n > 0 {
let cost_counts_even = cost_counts.iter().step_by(2).skip(1).sum::<usize>();
let cost_counts_odd = cost_counts.iter().skip(1).step_by(2).sum::<usize>();
total_count += if (steps - offset) & 1 == 0 {
(n + 1) / 2 * cost_counts_even + (n / 2) * cost_counts_odd
} else {
(n + 1) / 2 * cost_counts_odd + (n / 2) * cost_counts_even
};
}
for s in n + 1.. {
let count = grid::count_reachable(&costs, offset + (s - 1) * self.w, steps);
total_count += count;
if count == 0 {
break;
}
}
}
total_count
}
pub fn next_boundary(
&self,
boundary: &Boundary,
steps: usize,
) -> (Option<Boundary>, Vec<Steps>) {
let (off_c, fac_c, off_r, fac_r) = match boundary.heading {
Heading::East => (0, 0, self.h - 1, -1),
Heading::North => (self.w - 1, -1, self.h - 1, 0),
Heading::West => (self.w - 1, 0, 0, 1),
Heading::South => (0, 1, 0, 0),
};
let (mut queue, mut costs) = boundary
.data
.iter()
.enumerate()
.map(|(v, &d)| {
(
d.saturating_add(1),
(
off_c.wrapping_add_signed(fac_c * v as isize),
off_r.wrapping_add_signed(fac_r * v as isize),
),
)
})
.fold(
(BinaryHeap::new(), vec![Steps::MAX; self.w * self.h]),
|(mut heap, mut costs), (cost, (col, row))| {
heap.push((!cost, (col, row)));
costs[col + row * self.w] = cost;
(heap, costs)
},
);
while let Some((cost, (col, row))) = queue.pop() {
if boundary.offset == usize::MAX || boundary.offset + !cost as usize >= steps {
break;
}
// add adjacents
for (col, row) in [(1, 0), (0, -1), (-1, 0), (0, 1)]
.into_iter()
.map(|(dc, dr)| (col.wrapping_add_signed(dc), row.wrapping_add_signed(dr)))
.filter(|&(col, row)| {
(col < self.w && row < self.h) && self.data[col + row * (self.w + 1)] != b'#'
})
{
if costs[col + row * self.w] == Steps::MAX {
costs[col + row * self.w] = !cost + 1;
queue.push((cost - 1, (col, row)));
}
}
}
let next = Boundary::from_matrix(&costs, self.w, self.h, boundary.heading, boundary.offset);
((next.offset != usize::MAX).then_some(next), costs)
}
pub fn center_tile_costs(&self, steps: Steps) -> (Steps, Vec<Steps>) {
let start = self.get_start();
let mut costs = vec![Steps::MAX; self.w * self.h];
let mut queue = VecDeque::new();
costs[start.0 + start.1 * self.w] = 0;
queue.push_back((0, start));
while let Some((cost, (col, row))) = queue.pop_front() {
if cost >= steps {
break;
}
for (col, row) in [(1, 0), (0, -1), (-1, 0), (0, 1)]
.into_iter()
.map(|(dc, dr)| (col.wrapping_add_signed(dc), row.wrapping_add_signed(dr)))
.filter(|&(col, row)| {
(col < self.w && row < self.h) && self.data[col + row * (self.w + 1)] != b'#'
})
{
if costs[col + row * self.w] == Steps::MAX {
costs[col + row * self.w] = cost + 1;
queue.push_back((cost + 1, (col, row)));
}
}
}
let count = costs
.iter()
.filter(|&&c| c <= steps && (c & 1) == (steps & 1))
.count();
(count as _, costs)
}
pub fn center_tile_boundaries(&self, steps: usize) -> (usize, [Boundary; 4]) {
let (count, costs) = self.center_tile_costs(steps.min(Steps::MAX as _) as _);
(
count as _,
[
Boundary::from_matrix(&costs, self.w, self.h, Heading::East, 0),
Boundary::from_matrix(&costs, self.w, self.h, Heading::North, 0),
Boundary::from_matrix(&costs, self.w, self.h, Heading::West, 0),
Boundary::from_matrix(&costs, self.w, self.h, Heading::South, 0),
],
)
}
}
Day 22: Sand Slabs
Rust solution to AoC|2023|22.
Feels a bit like Tetris in 3D. I felt reminded of Aoc|2022|17, but in the end it was very different.
Input
I decided to create some struct types today. The input is parsed into a Vec of Brick elements. Each Brick is a pair of Point elements.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
pub mod input {
use crate::{Brick, Point};
#[derive(Debug)]
pub struct PuzzleData(pub Vec<Brick>);
impl From<&str> for Point {
fn from(value: &str) -> Self {
let mut values = value.split(',').map(|v| v.parse().unwrap());
Self {
x: values.next().unwrap(),
y: values.next().unwrap(),
z: values.next().unwrap(),
}
}
}
impl From<&str> for Brick {
fn from(value: &str) -> Self {
value
.split_once('~')
.map(|(a, b)| Self(a.into(), b.into()))
.unwrap()
}
}
impl<T> From<&T> for PuzzleData
where
T: AsRef<str> + ?Sized,
{
fn from(s: &T) -> Self {
Self(s.as_ref().lines().map(Brick::from).collect())
}
}
}
Star 1 & 2
Since settling the SandStack consumes an important part of the runtime (probably with a bit of room for optimization), I wanted to do it only once and implemented both solutions in one function.
Here is my lengthy solution. The key parts are
-
Build the sand stack and figure out which bricks are on top of each other; main parts implemented in
SandStack::from,Brick::compare. The compare function will also return the upperz-coordinate of the lower brick. -
Settle the stack, so that everything is touching either a brick below or solid ground:
SandStack::settleuses recursiveSandStack::settle_rec -
Solution to part 1 in
SandStack::count_disintegrateable -
Solution to part 2 in
SandStack::sum_count_falling- a kind of 'lowest-first-traversal'. Could maybe be optimized with some caching.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
pub type Coord = usize;
#[derive(Debug, PartialEq, Eq, PartialOrd, Ord, Clone, Copy)]
pub struct Point {
pub x: Coord,
pub y: Coord,
pub z: Coord,
}
#[derive(Debug, PartialEq, Eq, PartialOrd, Ord, Clone, Copy)]
pub struct Brick(pub Point, pub Point);
pub struct SandStack {
bricks: Vec<Brick>,
belows: Vec<Vec<(usize, Coord)>>,
}
trait Intersect {
fn intersect(&self, other: &Self) -> Self;
}
impl Intersect for RangeInclusive<Coord> {
fn intersect(&self, other: &Self) -> Self {
*self.start().max(other.start())..=*self.end().min(other.end())
}
}
impl From<(Coord, Coord, Coord)> for Point {
fn from((x, y, z): (Coord, Coord, Coord)) -> Self {
Self { x, y, z }
}
}
impl Brick {
pub fn compare(&self, other: &Self) -> Option<(Ordering, Coord)> {
if !self.x_range().intersect(&other.x_range()).is_empty()
&& !self.y_range().intersect(&other.y_range()).is_empty()
{
Some((
self.top_z().cmp(&other.top_z()),
self.top_z().min(other.top_z()),
))
} else {
None
}
}
pub fn x_range(&self) -> RangeInclusive<Coord> {
self.0.x.min(self.1.x)..=self.0.x.max(self.1.x)
}
pub fn y_range(&self) -> RangeInclusive<Coord> {
self.0.y.min(self.1.y)..=self.0.y.max(self.1.y)
}
pub fn top_z(&self) -> Coord {
self.0.z.max(self.1.z)
}
pub fn bottom_z(&self) -> Coord {
self.0.z.min(self.1.z)
}
}
impl From<&PuzzleData> for SandStack {
fn from(PuzzleData(bricks): &PuzzleData) -> Self {
let mut belows = vec![Vec::new(); bricks.len()];
for (k1, b1) in bricks.iter().enumerate() {
for (k2, b2) in bricks.iter().enumerate().skip(k1 + 1) {
match b1.compare(b2) {
Some((Ordering::Greater, b)) => belows[k1].push((k2, b)),
Some((_, b)) => belows[k2].push((k1, b)),
None => (),
}
}
}
let bricks = bricks.to_owned();
Self { bricks, belows }
}
}
impl SandStack {
fn settle_rec(&mut self, settled: &mut [bool], offsets: &mut [usize], k: usize) {
if settled[k] || self.bricks[k].bottom_z() == 1 {
return;
}
let z = (0..self.belows[k].len())
.map(|p| {
let (k2, _) = self.belows[k][p];
self.settle_rec(settled, offsets, k2);
let (_, ref mut z) = &mut self.belows[k][p];
*z -= offsets[k2];
*z
})
.max()
.unwrap_or(0);
let me = &mut self.bricks[k];
assert!(me.bottom_z() > z);
offsets[k] = me.bottom_z() - z - 1;
me.0.z -= offsets[k];
me.1.z -= offsets[k];
settled[k] = true;
}
pub fn settle(&mut self) {
let mut settled = vec![false; self.bricks.len()];
let mut offsets = vec![0; self.bricks.len()];
for k in 0..self.bricks.len() {
self.settle_rec(&mut settled, &mut offsets, k);
}
}
pub fn count_disintegrateable(&self) -> usize {
let mut unique_supporters = vec![false; self.bricks.len()];
for (k, me) in self.bricks.iter().enumerate() {
let supporters = self.belows[k]
.iter()
.filter(|(_, z)| z + 1 == me.bottom_z())
.map(|(p, _)| *p)
.take(2)
.collect::<Vec<_>>();
if supporters.len() == 1 {
unique_supporters[supporters[0]] = true;
}
}
self.bricks.len() - unique_supporters.into_iter().filter(|&s| s).count()
}
pub fn sum_count_falling(&self) -> usize {
// figure out what is supported above and what is supporting below
let mut supported = vec![Vec::new(); self.bricks.len()];
let mut supporting = vec![Vec::new(); self.bricks.len()];
for (k_above, (z_above, belows)) in (self.bricks.iter().map(Brick::bottom_z))
.zip(self.belows.iter())
.enumerate()
{
for &(k_below, _) in belows.iter().filter(|(_, z_below)| z_below + 1 == z_above) {
supported[k_below].push(k_above);
supporting[k_above].push(k_below);
}
}
// use binary heap (max heap) and sort by max z (inverted) to make
// sure we process bricks layer by layer
let mut queue = BinaryHeap::new();
let mut falling = HashSet::new();
let mut sum_count = 0;
for k_root in 0..self.bricks.len() {
falling.insert(k_root);
queue.push((!self.bricks[k_root].top_z(), k_root));
while let Some((_, k_below)) = queue.pop() {
for &k_above in supported[k_below].iter() {
if supporting[k_above].iter().all(|k| falling.contains(k))
&& falling.insert(k_above)
{
queue.push((!self.bricks[k_above].top_z(), k_above));
}
}
}
sum_count += falling.len() - 1; // do not count self
falling.clear();
}
sum_count
}
}
pub fn star_1_and_2(data: &PuzzleData) -> Solutions<usize, usize> {
let mut universe = SandStack::from(data);
universe.settle();
(
universe.count_disintegrateable(),
universe.sum_count_falling(),
)
.into()
}
Tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"1,0,1~1,2,1
0,0,2~2,0,2
0,2,3~2,2,3
0,0,4~0,2,4
2,0,5~2,2,5
0,1,6~2,1,6
1,1,8~1,1,9
"#;
#[test]
pub fn test_from() {
let data = PuzzleData::from(CONTENT);
let exp = vec![
Brick((1, 0, 1).into(), (1, 2, 1).into()),
Brick((0, 0, 2).into(), (2, 0, 2).into()),
Brick((0, 2, 3).into(), (2, 2, 3).into()),
Brick((0, 0, 4).into(), (0, 2, 4).into()),
Brick((2, 0, 5).into(), (2, 2, 5).into()),
Brick((0, 1, 6).into(), (2, 1, 6).into()),
Brick((1, 1, 8).into(), (1, 1, 9).into()),
];
assert_eq!(exp, data.0);
println!("{data:?}");
}
#[test]
pub fn test_star_1_and_2() {
assert_eq!((5, 7), star_1_and_2(&CONTENT.into()).into());
}
}
Day 23: A Long Walk
Rust solution to AoC|2023|23.
Input
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
pub mod input {
#[derive(Debug)]
pub struct PuzzleData<'a> {
pub data: &'a [u8],
pub w: usize,
pub h: usize,
}
impl<'a, T> From<&'a T> for PuzzleData<'a>
where
T: AsRef<[u8]> + 'a + ?Sized,
{
fn from(s: &'a T) -> Self {
let data = s.as_ref();
let w = data.iter().position(|&b| b == b'\n').unwrap_or(data.len());
let h = (data.len() + 1) / (w + 1);
Self { data, w, h }
}
}
}
Star 1
Shortest path - easy. But how do I get the longest path? Well, just try all of them…
The only interesting points in the grid are the start, the target and any coordinates, where there is actually a choice to make. So I build a grid that contains exactly those nodes with the unique distances to the neighbors as weights.
These are few enough for the problem to be solvable and to store the information which nodes have been seen in the bits of a u64.
The second part is the same as the first part. Just remove special treatment of slopes. This increases the number of edges in the graph and hence it runs a little longer.
Optimizations since initial version:
-
Modify graph: from the unique node from which the target is reachable, the only relevant adjacent is the target (idea from MattieShoes): from ~330ms to ~170ms
-
Prune nodes from where the target is not reachable using a graph traversal based on bit manipulations with a
u64as 'queue' (I especially like how adjacents are filtered and 'pushed to the queue' at once using bitwise operators): from ~170ms to ~150ms -
Prune nodes from where I have been before with the same set of reachable nodes but a longer distance walked (idea from boombulerDev): from ~150ms to ~40ms
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
pub type NodeT = (usize, usize);
impl PuzzleData<'_> {
const D: [(isize, isize, u8); 4] = [(1, 0, b'>'), (0, -1, b'^'), (-1, 0, b'<'), (0, 1, b'v')];
fn is_branch_point(&self, (col, row): NodeT) -> bool {
Self::D
.iter()
.map(|(dc, dr, _)| (col.wrapping_add_signed(*dc), row.wrapping_add_signed(*dr)))
.filter(|&(col, row)| {
col < self.w && row < self.h && self.data[col + row * (self.w + 1)] != b'#'
})
.count()
> 2
}
pub fn branch_points(&self) -> Vec<NodeT> {
(0..self.w * self.h)
.map(|pos| (pos % self.w, pos / self.w))
.filter(|&(col, row)| {
self.data[col + row * (self.w + 1)] != b'#'
&& (row == 0 || row == self.h - 1 || self.is_branch_point((col, row)))
})
.collect::<Vec<_>>()
}
fn adj_iter(
&self,
(col, row): NodeT,
ignore_slopes: bool,
) -> impl Iterator<Item = NodeT> + '_ {
Self::D
.iter()
.map(move |&(dc, dr, ok)| {
(col.wrapping_add_signed(dc), row.wrapping_add_signed(dr), ok)
})
.filter(move |&(col, row, ok)| {
col < self.w
&& row < self.h
&& (ignore_slopes && self.data[col + row * (self.w + 1)] != b'#'
|| [b'.', ok].contains(&self.data[col + row * (self.w + 1)]))
})
.map(|(col, row, _)| (col, row))
}
/// nodes are branch points and start (first) / target (last)
pub fn make_graph(
&self,
ignore_slopes: bool,
) -> (Vec<NodeT>, Vec<Vec<NodeT>>) {
let nodes = self.branch_points();
// calculate length of (unique) paths between all nodes
let mut adjacents = vec![Vec::new(); nodes.len()];
for (k0, &start) in nodes.iter().enumerate() {
let mut queue = Vec::from([(0, start, None)]);
while let Some((steps, cur, prev)) = queue.pop() {
if let Some(k1) = (cur != start)
.then_some(())
.and_then(|_| nodes.iter().position(|&coord| coord == cur))
{
adjacents[k0].push((k1, steps));
continue;
}
queue.extend(
self.adj_iter(cur, ignore_slopes)
.filter(|&adj| Some(adj) != prev)
.map(|adj| (steps + 1, adj, Some(cur))),
);
}
}
(nodes, adjacents)
}
}
pub fn reachable(adj_masks: &[u64], idx: usize, seen: u64) -> u64 {
let mut queue = 1u64 << idx;
let mut reached = seen | queue;
while queue != 0 {
let cur = queue.trailing_zeros();
queue &= !(1 << cur);
let mask = adj_masks[cur as usize];
queue |= mask & !reached;
reached |= mask;
}
reached & !seen
}
pub fn star(grid: &PuzzleData, ignore_slopes: bool) -> usize {
let (nodes, mut adjacents) = grid.make_graph(ignore_slopes);
// seen information is stored in bits of u64
assert!(nodes.len() <= 64);
let target = nodes.len() - 1;
if ignore_slopes {
// Idea taken from https://www.reddit.com/user/MattieShoes/
// At the last crossing before the target, we must go for the target
let (last_before_target, cost) = adjacents[target][0];
adjacents[last_before_target] = vec![(target, cost)];
}
let adj_masks: Vec<u64> = adjacents
.iter()
.map(|adjacents| adjacents.iter().fold(0, |mask, (adj, _)| mask | (1 << adj)))
.collect();
let mut bests = HashMap::new();
// find maximum
let mut queue = Vec::from([(0, 0, 1u64)]);
let mut max = 0;
while let Some((cost, idx, seen)) = queue.pop() {
if idx == target && cost > max {
max = cost;
continue;
}
// Efficient BFS to get reachable nodes
let reachable = reachable(&adj_masks, idx, seen);
if reachable & (1 << target) == 0 {
// Target is not reachable
continue;
}
// Idea taken from https://www.reddit.com/user/boombulerDev/
// If I have been here with the same set of reachable nodes, only expand node
// if it has a higher cost
match bests.entry((idx, reachable)) {
Entry::Occupied(o) if cost <= *o.get() => continue,
Entry::Occupied(mut o) => *o.get_mut() = cost,
Entry::Vacant(v) => _ = v.insert(cost),
}
queue.extend(
adjacents[idx]
.iter()
.filter(|(adj, _)| seen & (1 << adj) == 0)
.map(|&(adj, weight)| (cost + weight, adj, seen | 1 << adj)),
);
}
max
}
pub fn star_1(grid: &PuzzleData) -> usize {
star(grid, false)
}
pub fn star_2(grid: &PuzzleData) -> usize {
star(grid, true)
}
Tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"#.#####################
#.......#########...###
#######.#########.#.###
###.....#.>.>.###.#.###
###v#####.#v#.###.#.###
###.>...#.#.#.....#...#
###v###.#.#.#########.#
###...#.#.#.......#...#
#####.#.#.#######.#.###
#.....#.#.#.......#...#
#.#####.#.#.#########v#
#.#...#...#...###...>.#
#.#.#v#######v###.###v#
#...#.>.#...>.>.#.###.#
#####v#.#.###v#.#.###.#
#.....#...#...#.#.#...#
#.#########.###.#.#.###
#...###...#...#...#.###
###.###.#.###v#####v###
#...#...#.#.>.>.#.>.###
#.###.###.#.###.#.#v###
#.....###...###...#...#
#####################.#
"#;
#[test]
pub fn test_from() {
let data = PuzzleData::from(CONTENT);
println!("{data:?}");
}
#[test]
pub fn test_is_interesting() {
let data = PuzzleData::from(CONTENT);
assert!(data.is_branch_point((11, 3)));
assert!(!data.is_branch_point((4, 1)));
}
#[test]
pub fn test_star_1() {
assert_eq!(94, star_1(&CONTENT.into()));
}
#[test]
pub fn test_star_2() {
assert_eq!(154, star_2(&CONTENT.into()));
}
}
Day 24: Never Tell Me The Odds
Rust solution to AoC|2023|24.
Input
The hail-stones are represented as an array of pairs of position and velocity. Each array element represents one dimension.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
pub type Coord = i64;
pub type CoordE = i128;
#[derive(Default, Debug, PartialEq, Eq, Clone, Copy)]
pub struct PAndV<T> {
p: T,
v: T,
}
pub type Hail = [PAndV<Coord>; 3];
pub mod input {
use crate::Hail;
#[derive(Debug)]
pub struct PuzzleData(pub Vec<Hail>);
impl<T> From<&T> for PuzzleData
where
T: AsRef<str> + ?Sized,
{
fn from(s: &T) -> Self {
Self(
s.as_ref()
.lines()
.map(|line| {
line.split(&[',', '@'])
.map(str::trim)
.map(str::parse)
.map(Result::unwrap)
.enumerate()
.fold(Hail::default(), |mut h, (p, v)| {
*match p {
0..=2 => &mut h[p].p,
3..=5 => &mut h[p - 3].v,
_ => panic!(),
} = v;
h
})
})
.collect(),
)
}
}
}
Star 1
Part 1 is quite straight-forward. I calculate intersection points as rational numbers with numerator and denominator to avoid dealing with floating point numbers.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
const X: usize = 0;
const Y: usize = 1;
const Z: usize = 2;
pub fn intersect_2d(
h1: &Hail,
h2: &Hail,
x_range: &RangeInclusive<Coord>,
y_range: &RangeInclusive<Coord>,
) -> bool {
let h1 = h1.map(|PAndV { p, v }| PAndV {
p: p as CoordE,
v: v as CoordE,
});
let h2 = h2.map(|PAndV { p, v }| PAndV {
p: p as CoordE,
v: v as CoordE,
});
let d = h2[X].v * h1[Y].v - h1[X].v * h2[Y].v;
if d == 0 {
// parallel
h1[X].p == h2[X].p && h1[Y].p == h2[Y].p
} else {
let n1 = (h2[X].v * (h2[Y].p - h1[Y].p) - h2[Y].v * (h2[X].p - h1[X].p)) * d.signum();
let n2 = (h1[X].v * (h2[Y].p - h1[Y].p) - h1[Y].v * (h2[X].p - h1[X].p)) * d.signum();
let d = d.abs();
debug_assert_eq!(h1[X].p * d + h1[X].v * n1, h2[X].p * d + h2[X].v * n2);
debug_assert_eq!(h1[Y].p * d + h1[Y].v * n1, h2[Y].p * d + h2[Y].v * n2);
if n1 < 0 || n2 < 0 {
false
} else {
(*x_range.start() as CoordE * d..=*x_range.end() as CoordE * d)
.contains(&(h1[X].p * d + h1[X].v * n1))
&& (*y_range.start() as CoordE * d..=*y_range.end() as CoordE * d)
.contains(&(h1[Y].p * d + h1[Y].v * n1))
}
}
}
pub fn count_intersections_2d(
hails: &[Hail],
x_range: RangeInclusive<Coord>,
y_range: RangeInclusive<Coord>,
) -> usize {
hails
.iter()
.enumerate()
.map(|(k, h1)| {
hails[k + 1..]
.iter()
.filter(|&h2| intersect_2d(h1, h2, &x_range, &y_range))
.count()
})
.sum()
}
pub fn star_1(PuzzleData(hails): &PuzzleData) -> usize {
const RANGE: RangeInclusive<Coord> = 200_000_000_000_000..=400_000_000_000_000;
count_intersections_2d(hails, RANGE, RANGE)
}
Star 2
It took a long while until I figured that one out (and in the end, I needed a little hint from Reddit).
I still think, there is some beauty in the locus of potential solutions in a position-velocity plane for a single dimension. For a given rock velocity, we can even use the Chinese remainder theorem to find the rock position so that there will be a collision with every hail-stone. But all this did not lead anywhere…
Yet, because it looks nice: in the picture below, 'X' marks the position (horizontal axis, left to right) and velocity (vertical axis, bottom to top) of a hail-stone and each '#' marks position and velocity of a rock that collides at some positive time.
#.........#..............................
..#........#.............................
....#.......#............................
......#......#...........................
..#.....#.....#..........................
#....#....#....#.........................
#...#...#...#...#........................
..#..#..#..#..#..#.......................
#.#.#.#.#.#.#.#.#.#......................
####################.....................
....................X....................
.....................####################
......................#.#.#.#.#.#.#.#.#.#
.......................#..#..#..#..#..#..
........................#...#...#...#...#
.........................#....#....#....#
..........................#.....#.....#..
...........................#......#......
............................#.......#....
.............................#........#..
..............................#.........#The key insight was: if there is a unique solution, six equations should be enough to find it and we don’t need to take care to look at integer solutions only. In theory, any hail-stone adds one unknown (the time of collision) and contributes three equations (one for every dimension), so three hail-stones should be enough to come up with the 6 equations.
Unfortunately, those equations are non-linear. But if we look at pairs of hail-stones, we can get rid of the non-linear terms. So four hail-stones or three pairs result in 6 linear equations, that I solve with Gaussian elimination. See the comments in the code for details.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
pub fn solve<const N: usize, const M: usize>(mut mat: [[f64; M]; N]) -> [f64; N] {
assert!(M == N + 1, "M == N + 1 expected");
let mut h = 0;
let mut k = 0;
// gaussian eliminate
while h < N && k < M {
let i_max = (h..N)
.map(|i| (i, mat[i][k].abs()))
.max_by(|(_, v1), (_, v2)| v1.partial_cmp(v2).unwrap_or(Ordering::Equal))
.map(|(row, _)| row)
.unwrap();
if mat[i_max][k] == 0.0 {
k += 1;
} else {
(mat[i_max], mat[h]) = (mat[h], mat[i_max]);
for i in h + 1..N {
let f = mat[i][k] / mat[h][k];
mat[i][k] = 0.0;
for j in k + 1..M {
mat[i][j] -= mat[h][j] * f;
}
}
h += 1;
k += 1;
}
}
// calculate solution
let mut r = [0.0; N];
for k in (0..N).rev() {
r[k] = mat[k][M - 1] / mat[k][k];
for row in mat[0..k].iter_mut() {
row[M - 1] -= row[k] * r[k];
}
}
r
}
pub fn star_2(PuzzleData(hails): &PuzzleData) -> Coord {
// number of dimensions
const N: usize = 3;
// Base equations
// x[i] + t[i] vx[i] = xr + t[i] vxr
// y[i] + t[i] vy[i] = yr + t[i] vyr
//
// Eliminate t[i]
// (x[i] - xr) / (vxr - vx[i]) = (y[i] - yr) / (vyr - vy[i])
// (x[i] - xr) (vyr - vy[i]) - (y[i] - yr) (vxr - vx[i]) = 0
// This step creates additional solutions vxr = vx[i] and vyr = vy[i] with arbitrary
// x[i], y[i] and xr = x[i] and yr = y[i] with arbitrary vx[i], vy[i].
//
// Expanding and re-arranging terms yields
// vyr xr - vxr yr = vy[i] xr - vx[i] yr - y[i] vxr + x[i] vyr + (vx[i] y[i] - vy[i] x[i])
// ----LHS_xy----- ------------------------------RHS_xy[i]------------------------------
// where all nonlinear terms are on the left (LHS_xy), independent of i.
//
// RHS_xy[i] - RHS_xy[j] = 0 finally yields a linear equation in the unknowns
// xr, yr, vxr, vyr. Using four hailstones, we can construct 6 equations using
// RHS_xy[i] and RHS_yz[i] for 6 unknowns.
//
// What about the additional solutions introduced above by potentially multiplying by 0?
// - The problem has a unique solution
// - Any solution satisfies the equations (we do not remove solutions by multiplying by 0)
// => If the equations have a unique solution, it is the one we are looking for
let mut mat = [[0.0; 2 * N + 1]; 2 * N];
for k in 0..N {
let l = k + 1;
mat[k] = [
(hails[k][Y].v - hails[l][Y].v) as _,
(hails[l][Y].p - hails[k][Y].p) as _,
(hails[l][X].v - hails[k][X].v) as _,
(hails[k][X].p - hails[l][X].p) as _,
0.0,
0.0,
((hails[l][X].v * hails[l][Y].p - hails[l][Y].v * hails[l][X].p)
- (hails[k][X].v * hails[k][Y].p - hails[k][Y].v * hails[k][X].p)) as _,
];
mat[N + k] = [
0.0,
0.0,
(hails[k][Z].v - hails[l][Z].v) as _,
(hails[l][Z].p - hails[k][Z].p) as _,
(hails[l][Y].v - hails[k][Y].v) as _,
(hails[k][Y].p - hails[l][Y].p) as _,
((hails[l][Y].v * hails[l][Z].p - hails[l][Z].v * hails[l][Y].p)
- (hails[k][Y].v * hails[k][Z].p - hails[k][Z].v * hails[k][Y].p)) as _,
];
}
// solve the linear equations and transform to hail
let sol = solve(mat).map(|r| r.round() as Coord);
let r = [
PAndV {
p: sol[0],
v: sol[1],
},
PAndV {
p: sol[2],
v: sol[3],
},
PAndV {
p: sol[4],
v: sol[5],
},
];
// check solution on all points
debug_assert_eq!(
None,
hails
.iter()
.map(|&h| [0, 1, 2].map(|k| (h[k].p - r[k].p, r[k].v - h[k].v)))
.position(|deltas| {
// check t is the same for all coordinates with non-zero velocity delta
let (chk_1, _) = deltas
.into_iter()
.filter(|(_, v)| *v != 0)
.map(|(p, v)| p / v)
.fold((true, None), |(ok, cur_t), t| match (ok, cur_t) {
(false, _) => (false, None),
(_, None) => (t > 0, (t > 0).then_some(t)),
(_, Some(cur_t)) => (cur_t == t, (cur_t == t).then_some(cur_t)),
});
// ... and coordinate deltas are multiples of velocity deltas
let chk_2 = deltas
.into_iter()
.all(|(p, v)| v != 0 && p % v == 0 || v == 0 && p == 0);
!(chk_1 && chk_2)
})
.map(|idx| hails[idx]),
"Inconsistent solution"
);
r.into_iter().map(|c| c.p).sum()
}
Geometric solution
Choose three hail-stones, say A, B, and C. Denote the locus of A, B, and C as A(t) = xa + t dxa, B(t) = xb + t dxb, and C(t) = xc + t dxc.
Represent those in the inertial system of A, i.e., A is placed at the origin with zero velocity. Zero velocity is important, because this results in the rock to move through the origin at some time t_A to collide with A. The locus of the hail-stones in the inertial system of A are A'(t) = 0, B'(t) = xb' + t dxb', and C'(t) = xc' + t dxc' with vectors xb' = xb - xa, dxb' = dxb - dxa, xc' = xc - xa, and dxc' = dxc - dxa.
The locus of the rock is R'(t) = xr' + t dxr'. It necessarily passes through the origin for some time t_A. And it is supposed to intersect with the locus B'(t) and C'(t).
The rock locus R'(t) contains the origin and intersects with B'(t) (or C'(t) respectively) which does contain the origin, if and only if it is contained in the plane A-B that is spanned by A' (the origin) and B'(t) (or A-C spanned by A' and C'(t) respectively). Note that the surface which contains A'(t) and B'(t) (or C'(t) respectively) is a plane because A'(t) collapses to a single point (the origin) - otherwise, we would obtain nice little Hyperbolic paraboloids.
The rock locus R'(t) thus needs to be contained in the intersection of the two planes A-B and A-C. This determines the direction of the velocity vector dxr'', i.e., dxr' = n dxr'' for some n. If we assume that the coordinates of dxr' are integers and if we choose dxr'' such that the greatest common divisor of its three integer coordinates is 1, then n will be an integer.
The points of collision with B'(t) (or C'(t) respectively) can be determined by calculating t_b and k_b such that xb' + t_b dxb' = 0 + k_b dxr'' (or t_c and k_c such that xc' + t_c dxc' = 0 + k_c dxr''). If the problem is well posed, this yields an integer solution for t_b and k_b with t_b > 0 (or t_c and k_c with t_c > 0 respectively).
The two equations xr' + t_b dxr' = k_b dxr'' and xr' + t_c dxr' = k_c dxr'' can be solved for xr' and dxr': dxr' = n dxr'' with n = (k_c - k_b) / (t_c - t_b) and xr' = m dxr'' with m = (t_c k_b - t_b k_c) / (t_c - t_b).
The ideas are visualized in the picture below with A' (magenta, only one point), B' (blue), and C' (green), the first three hail-stones from the example given in the puzzle. Lines from A' to B'(0) and B'(1) (points depicted by squares) span the plane A-B, and lines from A' to C'(0) and C'(1) span A-C. Collision points are depicted by an X.
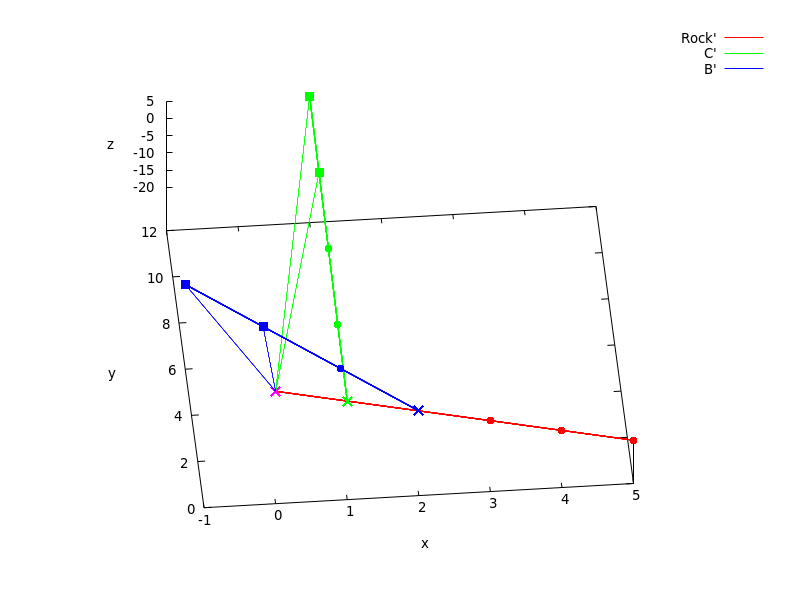
Tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"19, 13, 30 @ -2, 1, -2
18, 19, 22 @ -1, -1, -2
20, 25, 34 @ -2, -2, -4
12, 31, 28 @ -1, -2, -1
20, 19, 15 @ 1, -5, -3
"#;
#[test]
pub fn test_from() {
let PuzzleData(hails) = PuzzleData::from(CONTENT);
println!("{hails:?}");
assert_eq!(
vec![
[
PAndV { p: 19, v: -2 },
PAndV { p: 13, v: 1 },
PAndV { p: 30, v: -2 }
],
[
PAndV { p: 18, v: -1 },
PAndV { p: 19, v: -1 },
PAndV { p: 22, v: -2 }
],
[
PAndV { p: 20, v: -2 },
PAndV { p: 25, v: -2 },
PAndV { p: 34, v: -4 }
],
[
PAndV { p: 12, v: -1 },
PAndV { p: 31, v: -2 },
PAndV { p: 28, v: -1 }
],
[
PAndV { p: 20, v: 1 },
PAndV { p: 19, v: -5 },
PAndV { p: 15, v: -3 }
]
],
hails
);
}
#[test]
pub fn test_star_1() {
const RANGE: RangeInclusive<Coord> = 7..=27;
let PuzzleData(hails) = CONTENT.into();
assert_eq!(2, count_intersections_2d(&hails, RANGE, RANGE));
}
#[test]
pub fn test_star_2() {
assert_eq!(47, star_2(&CONTENT.into()));
}
}
Day 25: Snowverload
Rust solution to AoC|2023|25.
Input
Process the input into a Vec of Vec of adjacents (identified by index).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
mod input {
use std::collections::HashMap;
pub struct PuzzleData(pub Vec<Vec<usize>>);
impl From<&str> for PuzzleData {
fn from(value: &str) -> Self {
let mut adjacents = Vec::<Vec<usize>>::new();
let mut indices = HashMap::new();
for line in value.lines() {
let mut parts = line
.split::<&[char]>(&[' ', ':'])
.map(str::trim)
.filter(|v| !v.is_empty())
.map(|key| {
let idx = indices.len();
*indices.entry(key).or_insert(idx)
});
let key = parts.next().unwrap();
for value in parts {
adjacents.resize(adjacents.len().max(key + 1).max(value + 1), Vec::new());
adjacents[key].push(value);
adjacents[value].push(key);
}
}
Self(adjacents)
}
}
}
Star 1
My first attempt was to implement the Stoer-Wagner algorithm to find a minimum cut of the graph. It worked but only spew out a solution after 10 minutes! But the solution was quite generic. It did not need any knowledge on how many edges need to be removed, it just found the smallest number of edges so that their removal splits the graph in two parts.
My new solution uses the knowledge about the minimum number of edges to be removed.
We start by choosing an arbitrary start node (node at index 0).
Then we search a target node for which we can find exactly three disjoint paths from the start node. This target node and the start node will end up in distinct parts of the graph once split in two.
If those paths are removed from the graph, only the nodes in one partition remain reachable.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#[cfg(not(feature = "min-cut"))]
mod direct_solution {
use std::collections::{HashMap, HashSet, VecDeque};
pub fn get_shortest_path(
adjacents: &[Vec<usize>],
forbidden: &[Vec<(usize, usize)>],
start: usize,
target: usize,
) -> (Option<HashMap<usize, usize>>, usize) {
let mut seen = HashSet::from([start]);
let mut queue = VecDeque::from([start]);
let mut parents = HashMap::new();
let mut reached = 0;
while let Some(idx) = queue.pop_front() {
reached += 1;
if idx == target {
return (Some(parents), reached);
}
for &adj in adjacents[idx].iter().filter(|&&adj| {
!forbidden
.iter()
.any(|forbidden| forbidden.contains(&(adj.min(idx), adj.max(idx))))
}) {
if seen.insert(adj) {
queue.push_back(adj);
parents.insert(adj, idx);
}
}
}
(None, reached)
}
pub fn get_partitions_connected_by_three_paths(
adjacents: &[Vec<usize>],
start: usize,
) -> (usize, usize) {
let mut paths = [Vec::new(), Vec::new(), Vec::new()];
for target in 1..adjacents.len() - 1 {
// find three disjoint paths
for k in 0..3 {
let (Some(parents), _) = get_shortest_path(adjacents, &paths[0..k], start, target)
else {
panic!("Less than three paths from {} to {}!", start, target);
};
paths[k].clear();
let mut cur = target;
while let Some(&parent) = parents.get(&cur) {
let link = (cur.min(parent), cur.max(parent));
paths[k].push(link);
cur = parent;
}
}
// return partition sizes, if there is no fourth path
if let (None, reached) = get_shortest_path(adjacents, &paths, start, target) {
return (reached, adjacents.len() - reached);
}
}
panic!("No solution");
}
}
#[cfg(not(feature = "min-cut"))]
pub fn star_1(PuzzleData(adjacents): &PuzzleData) -> usize {
// get a size of partitions connected by three paths
let (p1, p2) = direct_solution::get_partitions_connected_by_three_paths(adjacents, 0);
p1 * p2
}
Tests
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#[cfg(test)]
mod tests {
use super::*;
const CONTENT: &str = r#"jqt: rhn xhk nvd
rsh: frs pzl lsr
xhk: hfx
cmg: qnr nvd lhk bvb
rhn: xhk bvb hfx
bvb: xhk hfx
pzl: lsr hfx nvd
qnr: nvd
ntq: jqt hfx bvb xhk
nvd: lhk
lsr: lhk
rzs: qnr cmg lsr rsh
frs: qnr lhk lsr
"#;
#[test]
pub fn test_star_1() {
assert_eq!(54, star_1(&CONTENT.into()));
}
}